-
Câu hỏi:
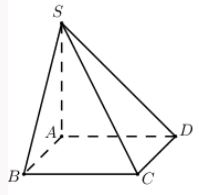
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\). Biết góc tạo bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng \(60^\circ \). Tính thể tích \(V\) của khối chóp \(S.ABCD\).
- A. \(V = {a^3}\sqrt 3 \).
- B. \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\).
- C. \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
- D. \(V = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).
Lời giải tham khảo:
Đáp án đúng: B
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SB \bot BC\\\left( {ABCD} \right) \supset AB \bot BC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA = {60^0}\)
Ta có: \(SA = AB\tan 60 = a\sqrt 3 \)\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .{a^2} = \dfrac{{{a^3}\sqrt 3 }}{3}\).
Chọn B.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Hàm số liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?
- Cho hàm số \(y = \dfrac{{2x}}{{x + 2}}\) có đồ thị \((C)\). Viết phương trình tiếp tuyến của \((C)\), biết tiếp tuyến tạo với hai trục tọa độ một tam giác có diện tích bằng \(\dfrac{1}{{18}}\).
- Cho hàm số\(y = (x - 2)({x^2} - 5x + 6)\) có đồ thị \(\left( C \right)\). Mệnh đề nào dưới đây đúng.
- Hàm số \(y = {x^4} - 8{x^2} - 4\) nghịch biến trên các khoảng.
- Cho khai triển \({\left( {1 - 2x} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}\) biết \(S = \left| {{a_1}} \right| + 2\left| {{a_2}} \right| + ... + n\left| {{a_n}} \right| = 34992\). Tính giá trị của biểu thức \(P = {a_0} + 3{a_1} + 9{a_2} + ... + {3^n}{a_n}\)
- Số đường tiệm cận của đồ thị hàm số\(y = \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 4}}\) là.
- Cho đồ thị của hàm số \(y = {x^3} - 6{x^2} + 9x - 2\) như hình vẽ. Khi đó phương trình \(\left| {{x^3} - 6{x^2} + 9x - 2} \right| = m\) (m là tham số) có 6 nghiệm phân biệt khi và chỉ khi.
- Cho khối lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Các điểm E và \(F\) lần lượt là trung điểm của C’B’ và C’D’.
- Gọi \(\left( {x;y} \right)\) là nghiệm dương của hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x + y} + \sqrt {x - y} = 4\\{x^2} + {y^2} = 128\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array} \right.\). Tổng \(x + y\) bằng:
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\). Cạnh bên \(SA\) vuông góc với mặt phẳng \((ABCD)\) và \(SA = a\). Góc giữa đường thẳng \(SB\) và \(CD\) là:
- Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn?
- Số nghiệm nguyên của bất phương trình\(\sqrt {2\left( {{x^2} - 1} \right)} \le x + 1\) là.
- Phương trình tiếp tuyến với đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) song song với đường thẳng \(\left( \Delta \right):\,\,2x + y + 1 = 0\) là.
- Chonj câu đúng. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
- Cho hàm số \(f\left( x \right)\) xác định trên R và có đồ thị hàm số \(y = f'\left( x \right)\) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
- Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Gọi \(P\) là xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ. Khi đó \(P\) bằng.
- Điểm cực tiểu của hàm số \(y = {x^3} - 3{x^2} - 9x + 2\).
- Cho hàm số \(y = f(x)\) có bảng biến thiên như bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA\( \bot \)(ABCD) và \(SB = \sqrt 3 \). Thể tích khối chóp S.ABCD là.
- Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3{x^2} - x + 3\) tại điểm \(M\left( {1;0} \right)\) là.
- Giá trị lớn nhất của hàm số \(y = \dfrac{{{x^2} - 3x}}{{x + 1}}\) trên đoạn \(\left[ {0;3} \right]\) bằng.
- Cho hàm số \(y = f\left( x \right) = \dfrac{1}{3}{x^3} - \left( {m + 1} \right){x^2} + \left( {m + 3} \right)x + m - 4\). Tìm để hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 điểm cực trị?
- Đồ thị hàm số \(y = \dfrac{{2x + 1}}{{x - 1}}\) có tiệm cận ngang là.
- Số cách xếp 5 người vào 5 vị trí ngồi thành hàng ngang là.
- Biết \({m_0}\) là giá trị của tham số m để hàm số \(y = {x^3} - 3{x^2} + mx - 1\) có hai điểm cực trị \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + x_2^2 - {x_1}{x_2} = 13\). Mệnh đề nào dưới đây đúng?
- Đồ thị cho dưới đây là của hàm số nào?
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,{\rm{ }}AD = 2a\), \(SA\) vuông góc với mặt phẳng\(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \). Thể tích của khối chóp \(S.ABCD\) là.
- Cho \(\sin \alpha = \dfrac{1}{3}\)và \(\dfrac{\pi }{2} < \alpha < \pi \). Khi đó \(\cos \alpha \) có giá trị là.
- \(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{ - 2x + 1}}{{x - 1}}\) bằng.
- Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng \(200{m^3}\) đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng.
- Có bao nhiêu giá trị nguyên m để đường thẳng \(\left( d \right):\,\,y = x - m\) cắt đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) tại hai điểm phân biệt A, B sao cho \(AB = 3\sqrt 2 \).
- Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình bên.Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m + 2\) có bốn nghiệm phân biệt.
- Gọi \(S\)là diện tích đáy, \(h\)là chiều cao. Thể tích khối lăng trụ là.
- Cho hàm số \(f(x)\) có đạo hàm \(f'(x)\) có đồ thị như hình vẽ. Hàm số \(g(x) = f(x) - \dfrac{{{x^3}}}{3} + {x^2} - x + 2\) đạt cực đại tại điểm nào?
- Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có đỉnh \(B( - 12;1)\), đường phân giác trong góc A có phương trình \(d:x + 2y - 5 = 0\).
- Đồ thị cho sau đây là của hàm số nào ?
- Cho hình chóp tam giác \(S.ABC\)với \(ABC\)là tam giác đều cạnh \(a\). \(SA \bot (ABC)\) và \(SA = a\sqrt 3 .\) Tính thể tích của khối chóp \(S.ABC\).
- Hỏi có tất cả bao nhiêu giá trị nguyên của m để đồ thị hàm số \(y = 2{x^3} - 3\left( {m + 3} \right){x^2} + 18mx - 8\) tiếp xúc với trục hoành?
- Gọi\(S\) là tập hợp các số nguyên \(m\) để hàm số \(y = f(x) = \dfrac{{x + 2m - 3}}{{x - 3m + 2}}\) đồng biến trên khoảng \(\left( { - \infty ; - 14} \right)\). Tính tổng \(T\) của các phần tử trong \(S\) ?
- Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\).
- Hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\). Khẳng định nào sau đây đúng.
- Chọn câu đúng. Thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a là.
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\).
- Giá trị cực tiểu của hàm số \(y = {x^4} - 2{x^2} - 3\)là.
- Phương trình \(\cos x = \cos \dfrac{\pi }{3}\) có nghiệm là:
- Hàm số \(y = - {x^3} - 3{x^2} + 9x + 20\) đồng biến trên các khoảng.
- Khoảng cách từ \(I(1; - 2)\) đến đường thẳng \(\Delta :3x - 4y - 26 = 0\) bằng.
- Để giá trị lớn nhất của hàm số \(y = \left| {\sqrt {2x - {x^2}} - 3m + 4} \right|\) đạt giá trị nhỏ nhất thì m thỏa.
- Cho hàm số \(y = f\left( x \right)\)liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hỏi hàm số \(g\left( x \right) = f\left( {{x^2} + 1} \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
- Thực hiện tính thể tích \(V\;\)của khối chóp có đáy là hình vuông cạnh \(2a\) và chiều cao là \(3a\)