Cho đường tròn (O) và hai điểm A,B nằm trên đường tròn. Kẻ đường kính AC,BD của đường tròn. Biết rằng OAB=45^0 và bán kính của đường tròn là 12cm.

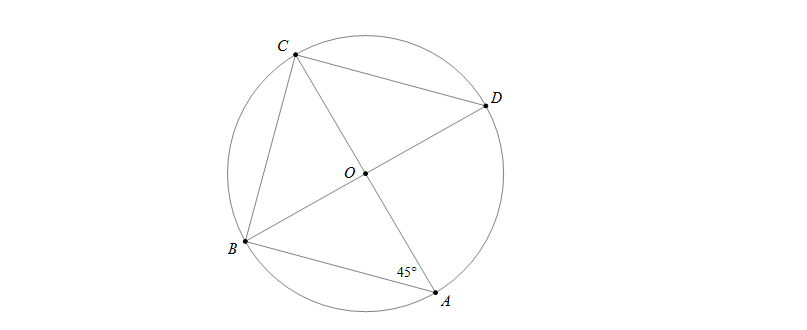
Trước hết ta thấy \(\widehat{COD}=\widehat{AOB}\) (đối đỉnh) nên \(\stackrel\frown{CD}=\stackrel\frown{AB}\), suy ra \(CD=AB\).

Do đó để tính độ dài CD, ta đưa về tính độ dài AB.

Xét tam giác OAB có OA=OB nên \(\bigtriangleup OAB\) cân tại O, do đó \(\widehat{OBA}=\widehat{OAB}=45^0\)

Từ đó suy ra \(\widehat{AOB}=90^0\Rightarrow \bigtriangleup AOB\) vuông cân tại O

Theo đề bài ta có OA=12cm, áp dụng định lí Pytago cho tam giác vuông AOB ta có: \(AB=\sqrt{OA^2+OB^2}=\sqrt{12^2+12^2}=12\sqrt{2} cm\)