I. Mô hình hành tinh nguyên tử
+ Năm 1911, Rutherford mạnh dạn đề sướng mẫu hành tinh nguyên tử.
+ Năm 1913, Niels Bosh (Bo) → Mẫu nguyên tử Bo.
II. Hai tiên đề Bo
1. Tiên đề về trạng thái dừng
- Nguyên tử chỉ tồn tại trong những trạng thái có NL hoàn toàn xác định, gọi là trạng thái dừng. Ở trạng thái dừng, nguyên tử không bức xạ.
+ Trong các trạng thái dừng, electron chuyển động trên những quỹ đạo hoàn toàn xác định gọi là quỹ đạo dừng.

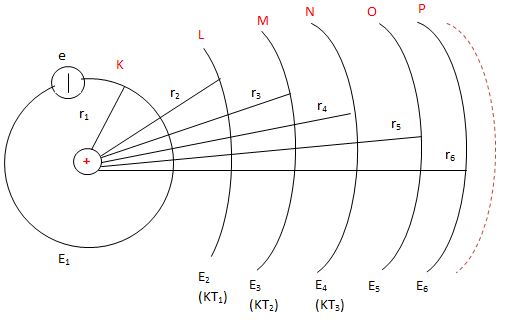
Với \(E_n=-\frac{13,6}{n^2} \ (eV)\)
\(\Rightarrow E_1=-13,6(eV);E_2=\frac{E_1}{4};E_3=\frac{E_1}{9};...\)
\(r_n=n^2.r_0;r_0=5,3.10^{-11}(m)\) bk Bo
\(\Rightarrow r_1=r_0;r_2=4.r_0=9r_0,...\)
2. Tiên đề về bức xạ và hấp thụ của nguyên tử.
- Khi nguyên tử ở trạng thái dừng có mức NL \(E_n\), nhảy về trạng thái dừng có mức NL, \(E_m\) thấp hơn thì phát ra 1 photon có NL \(E_{nm}=E_m-E_n\) và ngược lại.

III. Quang phổ vạch của Hidrô

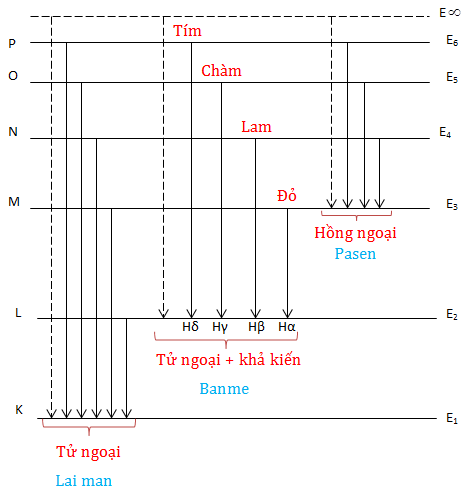
* Các dạng bài tập

1. Áp dụng công thức:
\(\left\{\begin{matrix} E_n=-\frac{13,6}{n^2}(eV)\\ r_n=n^2.r_0,r_0=5,3.10^{-11} \end{matrix}\right.\)
\(\varepsilon _{nm}=h.f{nm}=E_n-E_m=E_n-E_p+E_p-E_m=hf_{np}+hf_{pm}\)
\(\Rightarrow f_{nm}=f_{np}+f_{pm}=f_{np}-f_{mp}\)
\(\Rightarrow \frac{1}{ _{nm}}=\frac{1}{\lambda_{np}}+ \frac{1}{\lambda_{pm}}=\frac{1}{\lambda_{np}}-\frac{1}{\lambda_{mp}}\)
VD1: \(\frac{1}{\lambda _{32}}=\frac{1}{\lambda _{31}}-\frac{1}{\lambda _{21}}\)
2. Vận tốc của electron trên quỹ đạo dừng n:
Ta có: F_đt = F_ht \(\Rightarrow k.\frac{e^2}{r^2_m}=m.\frac{v^2}{r_m}\)
\(\Rightarrow v^2=\frac{k}{m}.\frac{e^2}{r_m}=\frac{k}{m}.\frac{e^2}{n^2.r_0}\)
\(\Rightarrow v=\frac{\left | e \right |}{n}.\sqrt{\frac{k}{m.r_0}}\)
VD1: Khi nguyên tử hidro ở trạng thái n thì năng lượng và bán kính được xác định \(E_n=-\frac{13,6}{n^2}\) và \(r_n=n^2.r_0\), với \(n_0=5,3.10^{-11}(m)\). Khi bán kính của electron bằng 2,12.10^-10 (m) thì năng lượng của nó bằng bao nhiêu?
Giải
Ta có
 \(r_n=n^2.r_0\)
\(\Rightarrow 2,12.10^{-10}=n^2.5,3.10^{-11}\Rightarrow n^2=4\)
⇒ Năng lượng \(E_n=\frac{13,6}{n^2}=-\frac{13,6}{4}=-3,4 \ eV\)
VD2: Khi nguyên tử hidro chuyển từ trạng thái E₄ về E₂ thì phát ra photon có bước sóng \(\lambda _{42}\). Khi nguyên tử hidro chuyển từ trạng thái E₅ về E3 thì phát ra photon có bước sóng \(\lambda _{53}\). Tìm \(\frac{\lambda _{53}}{\lambda _{42}}\) = ?
Giải
Ta có
\(\left.\begin{matrix} \varepsilon _{42}=\frac{hc}{\lambda _{42}}=E_4-E_2\\ \varepsilon _{53}=\frac{hc}{\lambda _{53}}=E_5-E_3 \end{matrix}\right\} \ \frac{\varepsilon _{42}}{\varepsilon _{53}}=\frac{\lambda _{53}} {\lambda _{42}}=\frac{E_4-E_2}{E_5-E_3}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{-\frac{13,6}{4^2} -(-\frac{13,6}{2^2})}{-\frac{13,6}{5^2}-(-\frac{13,6}{3^2})}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{-\frac{1}{4^2}+\frac{1}{2^2}} {-\frac{1}{5^2}+\frac{1}{3^2}}=\frac{675}{256}\)