1. Thí nghiệm về sự tán sắc ánh sáng của Niutơn

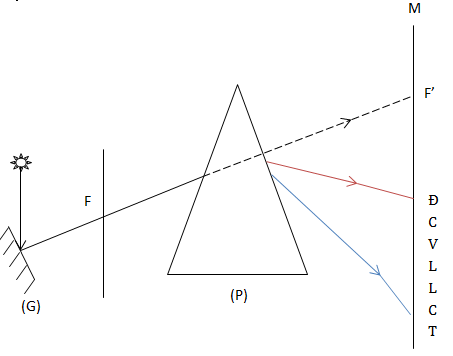
KL: Chiếu tia sáng hẹp từ mặt trời qua một lăng xích ⇒ tách ra một dải màu: Đỏ, cam, vàng, lục, lam, tràm, tím.
2. Thí nghiệm về ánh sáng đơn sắc của Niutơn.

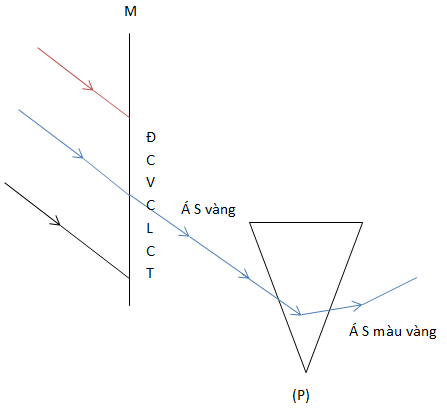
KL: Ánh sáng đơn sắc là ánh sáng có 1 màu nhất định và không bị tán sắc khi truyền qua lăng kính.
3. Giải thích
+ Ánh trắng (ánh sáng từ mặt trời, đèn dây tóc,...) là tập hợp vô số các ánh sáng đơn sắc có màu biến thiên liên tục từ đỏ đến tím.
+ Chiết suất của chất làm lăng kính (chất trong suốt: Rắn, lỏng, khí) thay đổi theo màu sắc ánh sáng, nhỏ nhất đối với ánh sáng đỏ và lớn nhất đối với ánh sáng tím.
+ Góc lệch: tăng theo chiết suất: D = A(n-1)
* Kết luận:
- Sự tán sắc ánh sáng là sự phân tách 1 chùm sáng phức tạp thành các chùm đơn sắc.
- Ánh sáng đơn sắc là ánh sáng có 1 màu nhất định và không bị tán sắc khi qua lăng kính
- Ánh sáng trắng là tập hợp vô số các ánh sáng đơn sắc có màu biến thiên từ đỏ sang tím.
4. Ứng dụng
+ Giải thích được hiện tương cầu vồng
+ Ứng dụng trong máy quang phổ lăng kính.
VD1: Một ánh sáng đơn sắc có bước sóng trong không khí là \(0,7\mu m\) và trong chất lỏng trong suôt là \(0,56\mu m\). Chiết suất của chất lỏng đối với ánh sáng đó bằng bao nhiêu?
Giải
+ Trong không khí:
\(n_1=\frac{c}{v_1}=\frac{c}{\lambda _1.f}=1\Rightarrow \lambda _1 = \frac{c}{f} (1)\)
+ Trong chất lỏng:
\(n_1=\frac{c}{v_2}=\frac{c}{\lambda _2.f}\Rightarrow \lambda _2 = \frac{c}{n_2.f} (2)\)
Từ (1) (2) \(\Rightarrow \lambda_2=\frac{\lambda_2}{n_2}\Rightarrow n_2=\frac{\lambda_1}{\lambda_2 }\Rightarrow n_2=\frac{0,7}{0,56}=1,25\)
* Nhớ: Trong môi trường có chiếc suất n thì bước sóng giảm n lần \(\Rightarrow \lambda '=\frac{\lambda }{n}\)
VD2: Chiếu 1 chùm tia sáng hẹp song song vào đỉnh của 1 lăng kính có góc chiết quang \(A=8^0\) theo phương vuông góc với mặt phẳng phân giác góc A. Chiết suất của lăng kính đối với ánh sáng đỏ và tím lần lượt là n_đ = 1,61 và n_t= 1,68. Màn hướng ánh đặt cách mặt phẳng phân giác 2m. Tìm bề rộng của quang phổ liên tục thu được trên màu?
Giải
\(A=8^0\); n_đ = 1,61, n_t= 1,68, d = 2 (m)

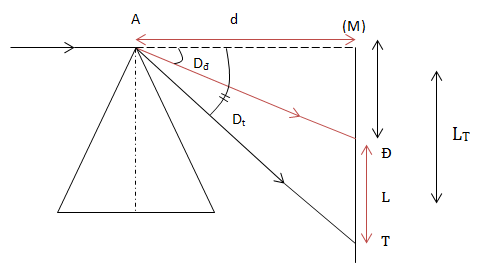
Ta có: L = L_T - L_Đ
D_đ = A(n_đ - 1) = \(\square\)
D_t = A(n_t - 1) = \(\bigtriangleup\)
tan Dđ = \(\frac{L_D}{d}\) ⇒ L_Đ = d tan D_đ
tan Dt = \(\frac{L_T}{d}\) ⇒ L_T = d tan D_t
⇒ L = L_T - L_Đ =d(tanD_t - tan D_đ)
⇒ L = 0, 196 (m)