I. Lý thuyết.
1. Khối lăng trụ - Khối chóp.
a) Khối lăng trụ
Hình lăng trụ:
+ 2 đáy là 2 đa giác bằng nhau.
+ Các cạch bên song song và bằng nhau.
+ Các mặt bên là các hình bình hành

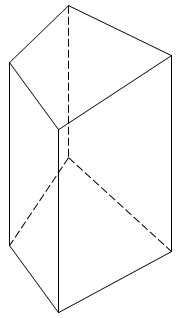
b) Khối chóp
Hình chóp:
+ Đáy là đa giác
+ Các mặt bên là các tam giác chung đỉnh.

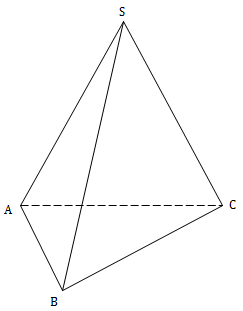
Khối chóp: Phần không gian được giới hạn được bởi hình chóp.
+ Đáy khối chóp là tam giác: khối chóp tam giác
+ Đáy khối chóp là tứ giác: khối chóp tam giác
+ Đáy khối chóp là ngũ giác: khối chóp tam giác
2. Khối đa diện.
Khối đa diện được giới hạn bởi hữu hạn đa giác thỏa mãn điều kiện.
(i) Hai đa giác bất kì không có điểm chung, hoặc có 1 điểm chung hoặc có chung 1 cạnh.
(ii) Mỗi cạnh đa giác là cạnh chung của đúng hai cạnh đa giác.
II. Bài tập
VD1: CMR một là đa diện có các mặt là những tam giác thì tổng số các mặt là số chẵn
Giải
Gọi số mặt đa diện là M
Gọi số cạnh đa diện là C
Do mỗi mặt là 1 tam giác nên số cạnh 3M.
Do mỗi cạnh đa giác là cạnh chung của đúng 2 mặt nên trong cách tính trên mỗi cạnh được lặp 2 lần.
Vậy ta có: 2C = 3M do (2, 3) = 1 nên M\(\vdots\) 2 hay M là số chẵn.
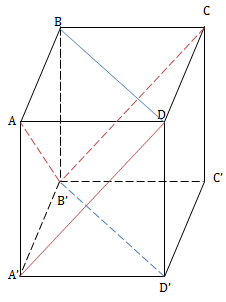
VD2: Chia khối hộp chữ nhật ABCD.A'B'C'D' thành 5 khối tứ diện.
Giải

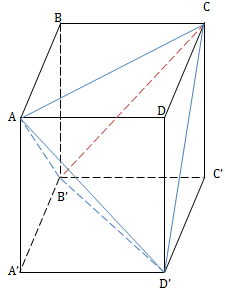
AA'B'D', D'ADC, CB'C'D', B'ABC, ACD'B'.
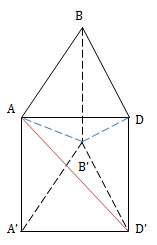
VD3: Chia khối lập phương ABCD.A'B'C'D' thành 6 khối tứ diện bằng nhau.
Giải

+ Chia khối lập phương thành 2 khối lăng trụ bằng nhau ABD.A'B'D' và CBD.C'B'D'. 
+ Chia mỗi khối lăng trụ thành 3 khói tứ diện bằng nhau ta được 6 khối tứ diện bằng nhau.
AA'B'D', B'ABD, AB'DD', CB'C'D', B'BCD, B'CC'D'