Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 257074
Có bao nhiêu cách chọn 2 học sinh từ 5 học sinh?
- A. 52
- B. 5!
- C. \(A_5^2\)
- D. \(C_5^2\)
-
Câu 2: Mã câu hỏi: 257075
Cho cấp số cộng có u1 = 1, u2 = -2. Chọn khẳng định đúng trong các khẳng định sau?
- A. d = 3
- B. d = -1
- C. u3 = -5
- D. u4 = 10
-
Câu 3: Mã câu hỏi: 257083
Tìm nghiệm của phương trình \({3^{x - 1}} = 1\).
- A. x = 1
- B. x = 4
- C. x = 0
- D. x = 3
-
Câu 4: Mã câu hỏi: 257085
Tính thể tích của một khối chóp biết khối chóp đó có đường cao bằng 6a, diện tích mặt đáy bằng 2a2.
- A. 4a2
- B. 4a3
- C. 12a3
- D. 12a2
-
Câu 5: Mã câu hỏi: 257089
Hàm số y = ax có đạo hàm là:
- A. ax
- B. axlna
- C. \(\frac{{{a^x}}}{{\ln a}}\)
- D. \({a^x}\ln x\)
-
Câu 6: Mã câu hỏi: 257100
Cho f(x), g(x) là các hàm số xác định và liên tục trên R. Trong các mệnh đề sau, mệnh đề nào sai?
- A. \(\int {f\left( x \right)g\left( x \right){\rm{d}}x = } \int {f\left( x \right){\rm{d}}x.\int {g\left( x \right){\rm{d}}x} } \)
- B. \(\int {2f\left( x \right){\rm{d}}x = 2} \int {f\left( x \right){\rm{d}}x} \)
- C. \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x = } \int {f\left( x \right){\rm{d}}x + \int {g\left( x \right){\rm{d}}x} } \)
- D. \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]{\rm{d}}x = } \int {f\left( x \right){\rm{d}}x - \int {g\left( x \right){\rm{d}}x} } \)
-
Câu 7: Mã câu hỏi: 257111
Cho hình lăng trụ đứng ABC.A'B'C' có AA' =4a, đáy ABC là tam giác đều cạnh a. Thể tích của khối lăng trụ là:
- A. a3
- B. \(\sqrt 3 {a^3}\)
- C. \(\frac{{\sqrt 3 }}{3}{a^3}\)
- D. 4a3
-
Câu 8: Mã câu hỏi: 257121
Cho khối nón có đường sinh bằng 5 và bán kính đáy bằng 3. Thể tích khối nón bằng
- A. \(18\pi \)
- B. \(12\pi \)
- C. \(24\pi \)
- D. \(15\pi \)
-
Câu 9: Mã câu hỏi: 257124
Công thức tính thể tích khối cầu có bán kính R là:
- A. $\frac{4}{3}\pi {R^3}
- B. \(\frac{3}{4}\pi {R^3}\)
- C. \(\frac{1}{3}\pi {R^3}\)
- D. \(4\pi {R^3}\)
-
Câu 10: Mã câu hỏi: 257471
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên
.png)
Mệnh đề nào trong các mệnh đề sau đây là mệnh đề đúng?
- A. Hàm số \(y=f\left( x \right)\) nghịch biến trên (-1;0) và \((1;+\infty )\).
- B. Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng \(\left( -1;1 \right)\).
- C. Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng \((-\infty ;-1)\) và (0;1).
- D. Hàm số \(y=f\left( x \right)\) đồng biến trên khoảng (-1;0) và \((1;+\infty )\).
-
Câu 11: Mã câu hỏi: 257474
Với a là số thực dương tùy ý, \({\log _3}\left( {{a^4}} \right)\) bằng:
- A. \(4{\log _3}a\)
- B. \(\frac{4}{3}{\log _3}a\)
- C. \(\frac{1}{4}{\log _3}a\)
- D. \(4 + {\log _3}a\)
-
Câu 12: Mã câu hỏi: 257475
Cho khối nón có bán kính đáy bằng r, chiều cao h. Thể tích V của khối nón là:
- A. \(V = \pi {r^2}h\)
- B. \(V = \frac{1}{3}\pi {r^2}h\)
- C. \(V = {r^2}h\)
- D. \(V = \frac{1}{3}{r^2}h\)
-
Câu 13: Mã câu hỏi: 257476
Cho hàm số y = f(x) có bảng biến thiên như sau:
.png)
Hàm số đã cho đạt cực tiểu tại
- A. x = 2
- B. x = 3
- C. x = -2
- D. x = 4
-
Câu 14: Mã câu hỏi: 257477
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
.jpg.png)
- A. \(y = {x^3} - 3x - 1\)
- B. \(y = - {x^3} - 3{x^2} - 1\)
- C. \(y = - {x^3} + 3{x^2} + 1\)
- D. \(y = {x^3} - 3x + 1\)
-
Câu 15: Mã câu hỏi: 257478
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 3}}\) là:
- A. y = 2
- B. y = 3
- C. x = 3
- D. \(x = \frac{1}{2}\)
-
Câu 16: Mã câu hỏi: 257479
Tập nghiệm của bất phương trình \({{\log }_{2}}x<3\) là
- A. \(\left( { - \infty ;8} \right)\)
- B. \(\left( {0; + \infty } \right)\)
- C. (0;8)
- D. \(\left( {8; + \infty } \right)\)
-
Câu 17: Mã câu hỏi: 257480
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
.png)
Số nghiệm của phương trình \(2f\left( x \right)-5=0\) là:
- A. 4
- B. 0
- C. 3
- D. 2
-
Câu 18: Mã câu hỏi: 257481
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_{1}^{2}{f\left( x \right)\text{d}x}=3\); \(\int\limits_{2}^{5}{f\left( x \right)\text{d}x}=-1\). Tính \(I=\int\limits_{1}^{5}{f\left( x \right)\text{d}x}\)
- A. I = 3
- B. I = 4
- C. I = 2
- D. I = -2
-
Câu 19: Mã câu hỏi: 257482
Cho số phức z=3+4i. Môđun của số phức z bằng:
- A. 3
- B. 5
- C. 7
- D. \(\sqrt 7 \)
-
Câu 20: Mã câu hỏi: 257483
Cho hai số phức \({{z}_{1}}=1+3i\) và \({{z}_{2}}=4-2i\). Phần ảo của số phức \({{z}_{1}}-{{z}_{2}}\) bằng
- A. 1
- B. -3
- C. 5
- D. -2
-
Câu 21: Mã câu hỏi: 257484
Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức
.jpg.png)
- A. \( - \frac{1}{2} + 2i\)
- B. - 1 + 2i
- C. 2 - i
- D. \(2 - \frac{1}{2}i\)
-
Câu 22: Mã câu hỏi: 257485
Trong không gian Oxyz, cho điểm \(A\left( 3;-1;1 \right)\). Hình chiếu vuông góc của A trên mặt phẳng x=1 là điểm
- A. (1;0;0)
- B. (1;-1;1)
- C. (0;-1;1)
- D. (0;0;1)
-
Câu 23: Mã câu hỏi: 257486
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right): {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y-8z+4=0\).Tính diện tích của mặt cầu \(\left( S \right)\)
- A. \(100\pi \)
- B. \(50\pi \)
- C. \(\frac{{500\pi }}{3}\)
- D. \(10\pi \)
-
Câu 24: Mã câu hỏi: 257487
Vectơ \(\vec{n}=\left( 1;2;-1 \right)\) là một vectơ pháp tuyến của mặt phẳng nào dưới đây?
- A. x + 2y + z + 2 = 0
- B. x + 2y - z - 2 = 0
- C. x + y - 2z + 1 = 0
- D. x - 2y + z + 1 = 0
-
Câu 25: Mã câu hỏi: 257489
Trong không gian Oxyz cho mặt phẳng \((P)\text{ }:x+y+z-2=0\). Điểm nào sau đây thuộc mặt phẳng (P)?
- A. N(2;-1;-3)
- B. P(5;-2;-1)
- C. Q(-1;0;-5)
- D. M(-2;1;1)
-
Câu 26: Mã câu hỏi: 257497
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy ABC là tam giác vuông tại B, AB=BC=a, \(BB'=a\sqrt{3}\). Tính góc giữa đường thẳng \({A}'B\) và mặt phẳng \(\left( BC{C}'{B}' \right)\).
- A. 45o
- B. 30o
- C. 60o
- D. 90o
-
Câu 27: Mã câu hỏi: 257500
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
.png)
Khẳng định nào sau đây là khẳng định đúng:
- A. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3
- B. Hàm số có đúng một cực trị.
- C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1
- D. Hàm số có giá trị cực tiểu bằng 2
-
Câu 28: Mã câu hỏi: 257502
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{2x + 1}}{{1 - x}}\) trên đoạn [2;3].
- A. 1
- B. -2
- C. 0
- D. -5
-
Câu 29: Mã câu hỏi: 257503
Cho các số thực dương a, b thỏa mãn \({{\log }_{2}}a=x, {{\log }_{2}}b=y\). Tính \(P={{\log }_{2}}\left( {{a}^{2}}{{b}^{3}} \right)\).
- A. \(P = {x^2}{y^3}\)
- B. \(P = {x^2} + {y^3}\)
- C. P = 6xy
- D. P = 2x + 3y
-
Câu 30: Mã câu hỏi: 257506
Cho hàm số \(y={{x}^{4}}+4{{x}^{2}}\) có đồ thị \(\left( C \right)\). Tìm số giao điểm của đồ thị \(\left( C \right)\) và trục hoành.
- A. 0
- B. 3
- C. 1
- D. 2
-
Câu 31: Mã câu hỏi: 257509
Tập nghiệm của bất phương trình \({\log ^2}x - 13\log x + 36 > 0\) là:
- A. \(T = \left( { - \infty ;\,4} \right) \cup \left( {9;\, + \infty } \right)\)
- B. \(T = \left( {0;\,4} \right] \cup \left[ {9;\, + \infty } \right)\)
- C. \(T = \left( {0;\,{{10}^4}} \right) \cup \left( {{{10}^9};\, + \infty } \right)\)
- D. \(T = \left( {{{10}^4};\,{{10}^9}} \right)\)
-
Câu 32: Mã câu hỏi: 257513
Trong không gian cho tam giác ABC vuông tại A có \(AB=\sqrt{3}\) và \(\widehat{ACB}={{30}^{\text{o}}}\). Tính thể tích V của khối nón nhận được khi quay tam giác ABC quanh cạnh AC.
- A. \(V = 3\pi \)
- B. \(V = 9\pi \)
- C. \(V = 12\pi \)
- D. \(V = \frac{{\sqrt 3 \pi }}{3}\)
-
Câu 33: Mã câu hỏi: 257516
Cho \(I=\int\limits_{0}^{4}{x\sqrt{1+2x\,}\text{d}x}\) và \(u=\sqrt{2x+1}\). Mệnh đề nào dưới đây sai?
- A. \(I = \frac{1}{2}\int\limits_1^3 {{x^2}\left( {{x^2} - 1} \right){\rm{d}}x} \)
- B. \(I = \int\limits_1^3 {{u^2}\left( {{u^2} - 1} \right){\rm{d}}u} \)
- C. \(I = \frac{1}{2}\left. {\left( {\frac{{{u^5}}}{5} - \frac{{{u^3}}}{3}} \right)} \right|_1^3\)
- D. \(I = \frac{1}{2}\int\limits_1^3 {{u^2}\left( {{u^2} - 1} \right){\rm{d}}u} \)
-
Câu 34: Mã câu hỏi: 257517
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{2x+1}{x-2}\); tiệm cận ngang và hai đường thẳng x=3;x=e+2 được tính bằng
- A. \(\int\limits_3^{e + 2} {\frac{{2x + 1}}{{x - 2}}dx} \)
- B. \(\int\limits_3^{e + 2} {\frac{5}{{x - 2}}dx} \)
- C. \(\left. {\ln \left| {x - 2} \right|} \right|_3^{e + 2}\)
- D. 5 - e
-
Câu 35: Mã câu hỏi: 257518
Cho hai số phức \({{z}_{1}}=3+i\) và \({{z}_{2}}=-1-5i\). Đặt \(w={{z}_{1}}.({{z}_{2}}+2i)\).Tìm |w|.
- A. 2
- B. 100
- C. \(2\sqrt {65} \)
- D. 10
-
Câu 36: Mã câu hỏi: 257521
Gọi \({{z}_{1}}\) là nghiệm phức có phần ảo âm thỏa mãn: \({{z}^{2}}+6z+13=0\). Tìm phần ảo của số phức \(w={{\left( i+1 \right)}^{2}}{{z}_{1}}\).
- A. 4
- B. -6
- C. -6i
- D. 4i
-
Câu 37: Mã câu hỏi: 257523
Viết phương trình mặt phẳng qua \(M\left( 1;-1;2 \right),N\left( 3;1;4 \right)\) và song song với trục Ox
- A. 3x + 4y + 4z - 7 = 0
- B. y + z = 0
- C. 4x - z + 1 = 0
- D. y - z + 3 = 0
-
Câu 38: Mã câu hỏi: 257527
Trong không gian với hệ trục Oxyz, cho tam giác ABC có \(A\left( -1;3;2 \right), B\left( 2;0;5 \right)\) và \(C\left( 0;-2;1 \right)\). Phương trình trung tuyến AM của tam giác ABC là.
- A. \(\frac{{x + 1}}{{ - 2}} = \frac{{y - 3}}{{ - 2}} = \frac{{z - 2}}{{ - 4}}\)
- B. \(\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 2}}{1}\)
- C. \(\frac{{x - 2}}{{ - 1}} = \frac{{y + 4}}{3} = \frac{{z - 1}}{2}\)
- D. \(\frac{{x - 1}}{2} = \frac{{y + 3}}{{ - 4}} = \frac{{z + 2}}{1}\)
-
Câu 39: Mã câu hỏi: 257531
Người ta muốn chia tập hợp 16 học sinh gồm 3 học sinh lớp 12A, 5 học sinh lớp 12B và 8 học sinh lớp 12C thành hai nhóm, mỗi nhóm có 8 học sinh. Xác suất sao cho ở mỗi nhóm đều có học sinh lớp 12A và mỗi nhóm có ít nhất hai học sinh lớp 12B là:
- A. \(\frac{{42}}{{143}}\)
- B. \(\frac{{84}}{{143}}\)
- C. \(\frac{{356}}{{1287}}\)
- D. \(\frac{{56}}{{143}}\)
-
Câu 40: Mã câu hỏi: 257539
Có bao nhiêu giá trị nguyên của m để hàm số \(y = {x^3} + 3{x^2} - \left( {{m^2} - 3m + 2} \right)x + 5\) đồng biến trên (0;2)?
- A. 3
- B. 2
- C. 4
- D. 1
-
Câu 41: Mã câu hỏi: 257542
Một người tham gia chương trình bảo hiểm HÀNH TRÌNH HẠNH PHÚC của công ty Bảo Hiểm MANULIFE với thể lệ như sau: Cứ đến tháng 9 hàng năm người đó đóng vào công ty là 12 triệu đồng với lãi suất hàng năm không đổi là 6%/ năm. Hỏi sau đúng 18 năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân.
- A. 403,32 (triệu đồng).
- B. 293,32 (triệu đồng).
- C. 412,23 (triệu đồng).
- D. 393,12 (triệu đồng).
-
Câu 42: Mã câu hỏi: 257547
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\). Hàm số luôn đồng biến trên R khi và chỉ khi
- A. \(\left[ \begin{array}{l} a = b = 0;\,c > 0\\ a > 0;\,{b^2} - 4ac \le 0\, \end{array} \right.\)
- B. \(a \ge 0;\,{b^2} - 3ac \le 0\)
- C. \(\left[ \begin{array}{l} a = b = 0;\,c > 0\\ a > 0;\,{b^2} - 3ac \ge 0 \end{array} \right.\)
- D. \(\left[ \begin{array}{l} a = b = 0;\,c > 0\\ a > 0;\,{b^2} - 3ac \le 0 \end{array} \right.\)
-
Câu 43: Mã câu hỏi: 257552
Cho hình thang ABCD vuông tại A và D, AD=CD=a, AB=2a. Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
- A. \(\frac{{5\pi {a^3}}}{3}\)
- B. \(\frac{{7\pi {a^3}}}{3}\)
- C. \(\frac{{4\pi {a^3}}}{3}\)
- D. \(\pi {a^3}\)
-
Câu 44: Mã câu hỏi: 257556
Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 1;4 \right]\), đồng biến trên đoạn \(\left[ 1;4 \right]\) và thỏa mãn đẳng thức \(x+2x.f\left( x \right) ={{\left[ {f}'\left( x \right) \right]}^{2}},\forall x\in \left[ 1;4 \right]\). Biết rằng \(f\left( 1 \right)=\frac{3}{2}\), tính \(I = \int\limits_1^4 {f\left( x \right){\rm{d}}x} \)?
- A. \(I = \frac{{1186}}{{45}}\)
- B. \(I = \frac{{1174}}{{45}}\)
- C. \(I = \frac{{1222}}{{45}}\)
- D. \(I = \frac{{1201}}{{45}}\)
-
Câu 45: Mã câu hỏi: 257558
Cho hàm số y=f(x) có bảng biến thiên như sau:
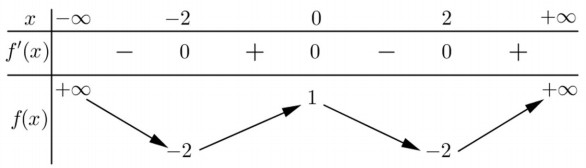
Số nghiệm thuộc đoạn \(\left[ -\pi ;\pi \right]\) của phương trình \(3f(2\sin x)+1=0\) là
- A. 4
- B. 5
- C. 2
- D. 6
-
Câu 46: Mã câu hỏi: 257559
Cho hai số thực x, y thỏa mãn: \(2{{y}^{3}}+7y+2x\sqrt{1-x}=3\sqrt{1-x}+3\left( 2{{y}^{2}}+1 \right)\).
Tìm giá trị lớn nhất của biểu thức P=x+2y.
- A. P = 8
- B. P = 10
- C. P = 4
- D. P = 6
-
Câu 47: Mã câu hỏi: 257566
Cho hàm số \(f\left( x \right)=\left| {{x}^{4}}-4{{x}^{3}}+4{{x}^{2}}+a \right|\). Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên \(\left[ 0;2 \right]\). Có bao nhiêu số nguyên a thuộc \(\left[ -4;4 \right]\) sao cho \(M\le 2m\)?
- A. 7
- B. 5
- C. 6
- D. 4
-
Câu 48: Mã câu hỏi: 257570
Cho khối tứ diện ABCD có thể tích 2020. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ
- A. \(\frac{{2020}}{9}\)
- B. \(\frac{{4034}}{{81}}\)
- C. \(\frac{{8068}}{{27}}\)
- D. \(\frac{{2020}}{{27}}\)
-
Câu 49: Mã câu hỏi: 257575
Giả sử a, b là các số thực sao cho \({{x}^{3}}+{{y}^{3}}=a{{.10}^{3z}}+b{{.10}^{2z}}\) đúng với mọi các số thực dương x, y, z thoả mãn \(\log \left( x+y \right)=z\) và \(\log \left( {{x}^{2}}+{{y}^{2}} \right)=z+1\). Giá trị của a+b bằng
- A. \(\frac{{31}}{2}\)
- B. \(\frac{{29}}{2}\)
- C. \(- \frac{{31}}{2}\)
- D. \( - \frac{{25}}{2}\)
-
Câu 50: Mã câu hỏi: 257579
Xét các số thực dương x,y thỏa mãn \(\ln \left( {\frac{{1 - 2x}}{{x + y}}} \right) = 3x + y - 1.\) Tìm giá trị nhỏ nhất Pmin của \(P = \frac{1}{x} + \frac{1}{{\sqrt {xy} }} + 1\)
- A. Pmin = 8
- B. Pmin = 16
- C. Pmin = 9
- D. Pmin = 2






