Dưới đây là Hướng dẫn giải bài tập Toán 12 nâng cao Ôn tập Chương 4 Số phức được hoc247 biên soạn và tổng hợp, nội dung bám sát theo chương trình SGK Toán 12 nâng cao giúp các em học sinh nắm vững phương pháp giải bài tập và ôn tập kiến thức hiệu quả hơn.
Bài 37 trang 208 SGK Toán 12 nâng cao
Tìm phần thực, phần ảo của
\(\begin{array}{l}
a){\left( {2 - 3i} \right)^3} \\
b)\frac{{3 + 2i}}{{1 - i}} + \frac{{1 - i}}{{3 - 2i}} \\
c)(x + iy)2 - 2(x + iy) + 5(x,y \in R)
\end{array}\)
Với x, y nào thì số phức đó là số thực?
Hướng dẫn giải:
Câu a:
\(\begin{array}{l}
{(2 - 3i)^3} = {2^3} - 3.2.3i(2 - 3i) - {(3i)^3}\\
= 8 - 18i(2 - 3i) + 27i = - 46 - 9i
\end{array}\)
Vậy phần thực là −46, phần ảo là −9
Câu b:
\(\begin{array}{l}
\frac{{3 + 2i}}{{1 - i}} = \frac{{(3 + 2i)(1 + i)}}{2} = \frac{{1 + 5i}}{2} = \frac{1}{2} + \frac{5}{2}i\\
\frac{{1 - i}}{{3 - 2i}} = \frac{{(1 - i)(3 + 2i)}}{{13}} = \frac{{5 - i}}{{13}} = \frac{5}{{13}} - \frac{1}{{13}}i
\end{array}\)
Do đó: \(\frac{{3 + 2i}}{{1 - i}} + \frac{{1 - i}}{{1 - i}} = \frac{1}{2} + \frac{5}{2}i + \frac{5}{{13}} - \frac{1}{{13}}i = \frac{{23}}{{26}} + \frac{{63}}{{26}}i\)
Vậy phần thực là 23/26, phần ảo là 63/26
Câu c:
\({(x + iy)^2} - 2(x + iy) + 5 = {x^2} - {y^2} - 2x + 5 + 2y(x - 1)i\)
Vậy phần thực là x2 − y2 − 2x + 5, phần ảo là 2y(x − 1)
Số phức đó là số thực khi vào chỉ khi 2y(x − 1) = 0 <=> y = 0 hoặc x = 1
Bài 38 trang 209 SGK Toán 12 nâng cao
Chứng minh rằng |z| = |w| = 1 thì số \(\frac{{z + w}}{{1 + zw}}\) là số thực (giả sử 1 + zw ≠ 0)
Hướng dẫn giải:
Ta có: \(z.\bar z = {\left| z \right|^2} = 1 \Rightarrow \bar z = \frac{1}{z}\)
Tương tự \(\overline w = \frac{1}{w}\)
Do đó: \(\overline {\left( {\frac{{z + {\rm{w}}}}{{1 + z{\rm{w}}}}} \right)} = \frac{{\bar z + {\rm{\bar w}}}}{{1 + \bar z.{\rm{\bar w}}}} = \frac{{\frac{1}{z} + \frac{1}{{\rm{w}}}}}{{1 + \frac{1}{z}.\frac{1}{{\rm{w}}}}} = \frac{{z + {\rm{w}}}}{{1 + z{\rm{w}}}}\)
Vậy \(\frac{{z + w}}{{1 + zw}}\) là số thực
Bài 39 trang 209 SGK Toán 12 nâng cao
Giải các phương trình sau trên C:
\(\begin{array}{l}
a)(z + 3 - i)2 - 6(z + 3 - i) + 13 = 0\\
b){\left( {\frac{{iz + 3}}{{z - 2i}}} \right)^2} - 3\frac{{iz + 3}}{{z - 2i}} - 4 = 0\\
c){({z^2} + 1)^2} + {(z + 3)^2} = 0
\end{array}\)
Hướng dẫn giải:
Câu a:
Đặt w = z + 3 − i ta được phương trình:
\(\begin{array}{l}
{w^2} - 6w + 13 = 0 \Leftrightarrow {(w - 3)^2} = - 4 = 4{i^2}\\
\Leftrightarrow \left[ \begin{array}{l}
w = 3 + 2i\\
w = 3 - 2i
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
z + 3 - i = 3 + 2i\\
z + 3 - i = 3 - 2i
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
z = 3i\\
z = - i
\end{array} \right.
\end{array}\)
Vậy S = {−i; 3i}
Câu b:
Đặt \(w = \frac{{iz + 3}}{{z - 2i}}\) ta được phương trình \({w^2} - 3w - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}
w = - 1\\
w = 4
\end{array} \right.\)
Với w = -1 ta có: \(\frac{{iz + 3}}{{z - 2i}} = - 1 \Leftrightarrow iz + 3 = - z + 2i\)
\( \Leftrightarrow (i + 1)z = - 3 + 2i \Leftrightarrow z = \frac{{ - 3 + 2i}}{{1 + i}} = \frac{{( - 3 + 2i)(1 - i)}}{2} = \frac{{ - 1 + 5i}}{2}\)
Với w = 4 ta có \(\frac{{iz + 3}}{{z - 2i}} = 4 \Leftrightarrow (4 - i)z = 3 + 8i\)
\( \Leftrightarrow z = \frac{{3 + 8i}}{{4 - i}} = \frac{{(3 + 8i)(4 + i)}}{{17}} = \frac{{4 + 35i}}{{17}}\)
Vậy \(S = \left\{ {\frac{{ - 1 + 5i}}{2};\frac{{4 + 35}}{{17}}} \right\}\)
Câu c:
\({({z^2} + 1)^2} + {(z + 3)^2} = {({z^2} + 1)^2} - {[i(z + 3)]^2}\)
\(\begin{array}{l}
= ({z^2} + 1 + i(z + 3))({z^2} + 1 - i(z + 3)) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{z^2} + 1 + i(z + 3) = 0(1)\\
{z^2} + 1 - i(z + 3) = 0(2)
\end{array} \right.
\end{array}\)
Phương trình (1) là phương trình bậc hai z2 + iz + 1 + 3i = 0
Δ = −5 − 12i = (2 − 3i)2
Phương trình có hai nghiệm là z1 = 1 − 2i và z2 = −1 + iz
Phương trình (2) là phương trình bậc hai z2 − iz + 1 − 3i = 0
Δ = − 5+ 12i = (2 + 3i)2
Phương trình có hai nghiệm là z3 = 1 + 2i và z4 = −1 − i
Vậy S={1 − 2i; −1 + i; 1 + 2i; −1−i}
Bài 40 trang 209 SGK Toán 12 nâng cao
Xét các số phức \({z_1} = \sqrt 6 - i\sqrt 2 ;{z_2} = - 2 - 2i;{z_3} = \frac{{{z_1}}}{{{z_2}}}\)
a) Viết \({z_1};{z_2}; {z_3}\) dưới dạng lượng giác
b) Từ câu a hãy tính \(\cos \frac{{7\pi }}{{12}}\) và \(\sin \frac{{7\pi }}{{12}}\)
Hướng dẫn giải:
Câu a:
\(\begin{array}{l}
{z_1} = \sqrt 2 (\sqrt 3 - i) = 2\sqrt 2 \left[ {cos\left( { - \frac{\pi }{6}} \right) + isin\left( { - \frac{\pi }{6}} \right)} \right]\\
{z_2} = 2( - 1 - i) = 2\sqrt 2 \left[ {cos\left( { - \frac{{3\pi }}{4}} \right) + isin\left( { - \frac{{3\pi }}{4}} \right)} \right]\\
{z_3} = \frac{{{z_1}}}{{{z_2}}} = cos\left( { - \frac{\pi }{6} + \frac{{3\pi }}{4}} \right) + isin\left( { - \frac{\pi }{6} + \frac{{3\pi }}{4}} \right)\\
= cos\left( {\frac{{7\pi }}{{12}}} \right) + isin\left( {\frac{{7\pi }}{{12}}} \right)
\end{array}\)
Câu b:
\(\frac{{{z_1}}}{{{z_2}}} = \frac{{\sqrt 6 - i\sqrt 2 }}{{ - 2 - 2i}} = \frac{{{z_1}}}{{{z_2}}} = \frac{{\sqrt 6 - i\sqrt 2 }}{{ - 2 - 2i}} = \frac{{\left( {\sqrt 6 - i\sqrt 2 } \right)\left( { - 2 + 2i} \right)}}{8} = \frac{{ - \sqrt 6 + \sqrt 2 }}{4} + \frac{{\sqrt 6 + \sqrt 2 }}{4}i\) nên so sánh với kết quả câu a, ta suy ra:
\(\cos \frac{{7\pi }}{{12}} = \frac{{ - \sqrt 6 + \sqrt 2 }}{4};\sin \frac{{7\pi }}{{12}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
Bài 41 trang 209 SGK Toán 12 nâng cao
Cho \(z = (\sqrt 6 + \sqrt 2 ) + i(\sqrt 6 - \sqrt 2 )\)
a) Viết z2 dưới dạng đại số và dưới dạng lượng giác
b) Từ câu a, hãy suy ra dạng lượng giác của z
Hướng dẫn giải:
Câu a:
\(\begin{array}{l}
{z^2} = {(\sqrt 6 + \sqrt 2 )^2} - {(\sqrt 6 - \sqrt 2 )^2} + 2i(\sqrt 6 + \sqrt 2 )(\sqrt 6 - \sqrt 2 )\\
= 4\sqrt {12} + 2i(6 - 2) = 8\sqrt 3 + 8i = 16\left( {cos\frac{\pi }{6} + isin\frac{\pi }{6}} \right)
\end{array}\)
Câu b:
Theo ứng dụng 2 của công thức Moa – vrơ, để ý rằng phần thực và phần ảo của z đều dương, suy ra \(z = 4\left( {cos\frac{\pi }{{12}} + isin\frac{\pi }{{12}}} \right)\)
Bài 42 trang 209 SGK Toán 12 nâng cao
a) Bằng cách biểu diễn hình học các số phức 2 + i và 3 + i, hãy chứng minh rằng nếu \(tana = \frac{1}{2},tanb = \frac{1}{3}\) với \(a,b \in \left( {0;\frac{\pi }{2}} \right)\) thì \(a + b = \frac{\pi }{4}\)
b) Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng nếu \(tana = \frac{1}{2},tanb = \frac{1}{5}\), \(\tan c = \frac{1}{8}\) với \(a,b,c \in \left( {0;\frac{\pi }{2}} \right)\) thì \(a + b + c= \frac{\pi }{4}\)
Hướng dẫn giải:
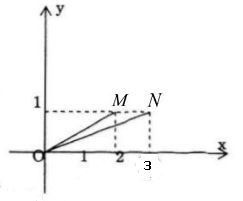
Câu a:
Biểu diễn hình học 2+i,3+i2+i,3+i theo thứ tự bới M và N trong mặt phẳng phức, ta có:
\(\begin{array}{l}
tan(Ox,OM) = \frac{1}{2} = tana\\
tan(Ox,ON) = \frac{1}{3} = tanb
\end{array}\)
Xét \(z.z' = (2 + i).(3 + i) = 5(1 + i)\)
\( = 5\sqrt 2 \left( {\cos \frac{\pi }{4} + i\sin \frac{\pi }{4}} \right)\)
Số zz′ có acgumen là π/4, suy ra \(a + b = \frac{\pi }{4}\)
Câu b:
z1 = 2 + i có một acgumen là a với tana = 1/2
z2 = 5 + i có một acgumen là b với tanb = 1/5
z3 = 8 + i có một acgumen là c với tanc = 1/8
Xét \(z = {z_1}{z_2}{z_3} = \left( {2 + i} \right)\left( {5 + i} \right)\left( {8 + i} \right) = 65\left( {1 + i} \right)\)
\( = 65\sqrt 2 \left( {\frac{{\sqrt 2 }}{2} + i\frac{{\sqrt 2 }}{2}} \right) = 65\sqrt 2 \left( {cos\frac{\pi }{4} + isin\frac{\pi }{4}} \right)\)
Số z có acgumen là π/4, suy ra \(a + b + c = \frac{\pi }{4}\)
Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Toán 12 Ôn tập Chương 4 Số phức được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 học tập thật tốt!
Tư liệu nổi bật tuần
- Xem thêm







