Giải Toán 10 SGK nâng cao Ôn tập Chương 3 Phương pháp tọa độ trong mặt phẳng

Xét vị trí tương đối của các đường thẳng Δ₁ và Δ₂ trong mỗi trường hợp sau

a) Δ₁: 3x−2y+1 = 0 và Δ₂: 2x+3y−5 = 0;

b) \({\Delta _1}:\left\{ \begin{array}{l}
x = 4 + 2t\\
y =  - 1 + t
\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}
x = 7 - 4t'\\
y = 5 - 2t'
\end{array} \right.\)

c) \({\Delta _1}:\left\{ \begin{array}{l}
x = 3 + 4t\\
y =  - 2 - 5t
\end{array} \right.\) và Δ₂: 5x+4y−7 = 0.

Hướng dẫn giải:

Câu a:

Ta có \(\frac{3}{2} \ne  - \frac{2}{3}\) nên Δ₁ và Δ₂ cắt nhau.

Câu b:

Phương trình tổng quát của Δ₁ và Δ₂ là

Δ₁: x−2y−6 = 0

Δ₂: x−2y+3 = 0

Ta có \(\frac{1}{1} = \frac{{ - 2}}{{ - 2}} \ne \frac{{ - 6}}{3}\) nên  Δ₁ // Δ₂

Câu c:

Phương trình tổng quát của Δ₁ là 5x+4y−7 = 0. Do đó Δ₁ ≡ Δ₂

---

Cho đường thẳng  Δ: 3x−4y+2 = 0.

a) Viết phương trình của Δ dưới dạng tham số.

b) Viết phương trình của Δ dưới dạng phương trình theo đoạn chắn.

c) Tính khoảng cách từ mỗi điểm M(3;5), N(−4;0), P(2;1) tới Δ và xét xem đường thẳng cắt cạnh nào của tam giác MNP.

d) Tính góc hợp bởi Δ và mỗi trục tọa độ.

Hướng dẫn giải:

Câu a:

Δ có vec tơ pháp tuyến là \(\overrightarrow n  = \left( {3; - 4} \right)\) nên có vec tơ chỉ phương là \(\overrightarrow u  = \left( {4;3} \right)\).

Δ đi qua điểm \(A\left( {0;\frac{1}{2}} \right)\). Vậy Δ có phương trình tham số là:

\(\left\{ \begin{array}{l}
x = 4t\\
y = \frac{1}{2} + 3t
\end{array} \right.\)

Câu b:

Phương trình đoạn chắn:

\(3x - 4y + 2 = 0 \Leftrightarrow 3x - 4y =  - 2 \Leftrightarrow \frac{x}{{ - \frac{2}{3}}} + \frac{y}{{\frac{1}{2}}} = 1\)

3x−4y+2 = 0 ⇔ 3x−4y = −2

\( \Leftrightarrow \frac{x}{{ - \frac{2}{3}}} + \frac{y}{{\frac{1}{2}}} = 1\)

Câu c:

Ta có: 

\(\begin{array}{l}
d\left( {M,\Delta } \right) = \frac{{\left| {3.3 - 4.5 + 2} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{9}{2}\\
d\left( {N,\Delta } \right) = \frac{{\left| {3.\left( { - 4} \right) + 2} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2\\
d\left( {P,\Delta } \right) = \frac{{\left| {3.2 - 4.1 + 2} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{4}{5}
\end{array}\)

M và N cùng phía đối với đường thẳng Δ còn P nằm khác phía nên Δ không cắt MN, Δ cắt MP và NP.

Câu d:

Đường thẳng Ox có phương trình  y = 0, α là góc giữa α với Ox thì

\(\cos \alpha  = \frac{{\left| {3.0 - 4.1} \right|}}{{\sqrt {{3^2} + {4^2}} .\sqrt {{0^2} + {1^2}} }} = \frac{4}{5} \Rightarrow \alpha  \approx {36^0}52'\)

Phương trình đường thẳng Oy là x = 0, β là góc giữa Δ với Oy ta có:

\(\cos \beta  = \frac{{\left| {3.1 - 4.0} \right|}}{{\sqrt {{3^2} + {4^2}} .\sqrt {{1^2} + {0^2}} }} = \frac{3}{5} \Rightarrow \beta  \approx {53^0}7'\)

---

Cho đường thẳng d: x−y+2 = 0 và điểm A(2;0)

a) Với điều kiện nào của x và y thì điểm M(x, y) thuộc nửa mặt phẳng có bờ d và chứa gốc tọa độ O? Chứng minh điểm A nằm trong nửa mặt phẳng đó.

b) Tìm điểm đối xứng với điểm O qua đường thẳng d.

c) Tìm điểm M trên d sao cho chu vi tam giác OMA nhỏ nhất.

Hướng dẫn giải:

 

Câu a:

Điểm M và O nằm cùng phía đối với d khi và chỉ khi

(x−y+2).(0−0+2) > 0 ⇔ x−y+2 > 0

Ta có : x_A−y_A+2 = 2−0+2 = 4 > 0, do đó A nằm trong nửa mặt phẳng có bờ là d và chứa O.

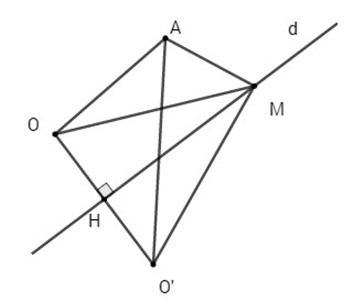
Câu b:

Gọi d’ là đường thẳng qua O và vuông góc với d thì phương trình tổng quát của d’ là  d′: x+y = 0. Gọi H là hình chiếu của O lên d thì tọa độ H là nghiệm của hệ:

\(\left\{ \begin{array}{l}
x - y =  - 2\\
x + y = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x =  - 1\\
y = 1
\end{array} \right.\)

Vậy H(−1;1)

Gọi O’ là điểm đối xứng của O qua d thì H là trung điểm của OO’ do đó

\(\left\{ \begin{array}{l}
{x_H} = \frac{{{x_O} + {x_{O'}}}}{2}\\
{y_H} = \frac{{{y_O} + {y_{O'}}}}{2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_{O'}} = 2{x_H} - {x_O} =  - 2\\
{y_{O'}} = 2{y_H} - {x_O} = 2
\end{array} \right.\)

Vậy O′(−2;2)

Câu c:

OA không đổi nên chu vi tam giác AMO nhỏ nhất  khi tổng MO+MA nhỏ nhất.

Ta có: MO = MO′ ⇒ MO+MA = MO′+MA ≥ AO′

⇒ MO+MA nhỏ nhất khi A, M, O’ thẳng hàng, khi đó M là giao điểm của d với đường thẳng O’A.

Phương trình O’A:

\(\begin{array}{l}
\frac{{x - {x_A}}}{{{x_{O'}} - {x_A}}} = \frac{{y - {y_A}}}{{{y_{O'}} - {y_A}}}\\
 \Leftrightarrow \frac{{x - 2}}{{ - 2 - 2}} = \frac{{y - 0}}{{2 - 0}}\\
 \Leftrightarrow x + 2y - 2 = 0
\end{array}\)

Tọa độ M là nghiệm của hệ: 

\(\left\{ \begin{array}{l}
x - y =  - 2\\
x + 2y = 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x =  - \frac{2}{3}\\
y = \frac{4}{3}
\end{array} \right.\)

Vậy \(M\left( { - \frac{2}{3};\frac{4}{3}} \right)\)

---

Cho đường thẳng Δ: ax+by+c = 0 và điểm I(x₀;y₀).Viết phương trình đường thẳng  đối xứng với đường thẳng Δ qua I. 

Hướng dẫn giải:

Đường thẳng Δ' đối xứng với đường thẳng Δ qua  I thì Δ // Δ' do đó phương trình tổng quát của Δ' có dạng ax+by+c′ = 0 (c′ ≠ c).Ta có:

\(\begin{array}{l}
d\left( {I,\Delta } \right) = d\left( {I,\Delta '} \right)\\
 \Leftrightarrow \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {a{x_0} + b{y_0} + c'} \right|}}{{\sqrt {{a^2} + {b^2}} }}\\
 \Leftrightarrow \left[ \begin{array}{l}
a{x_0} + b{y_0} + c = a{x_0} + b{y_0} + c'\\
a{x_0} + b{y_0} + c =  - a{x_0} - b{y_0} - c'
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
c = c'\\
c' =  - c - 2\left( {a{x_0} + b{y_0}} \right)
\end{array} \right.
\end{array}\)

Loại trường hợp c = c′.

Vậy Δ′: ax+by−c−2(ax_o+by_o+c) = 0

---

Một hình bình hành có hai cạnh nằm trên hai đường thẳng x + 3y - 6 = 0 và 2x - 5y - 1 = 0. Biết hình bình hành đó có tâm đối xứng là I(3;5). Hãy viết phương trình hai cạnh còn lại của hình bình hành đó.

Hướng dẫn giải:

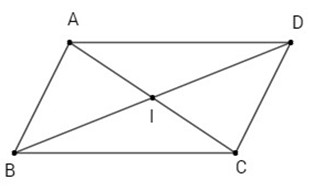
Giả sử hình bình hành ABCD có tâm I

AB: x+3y−6 = 0

AD: 2x−5y−1 = 0

Tọa độ của A là nghiệm của hệ:

\(\left\{ \begin{array}{l}
x + 3y - 6 = 0\\
2x - 5y - 1 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 3\\
y = 1
\end{array} \right.\)

Vậy A(3;1).

Vì I là trung điểm của AC nên:

\(\left\{ \begin{array}{l}
{x_I} = \frac{1}{2}\left( {{x_A} + {x_C}} \right)\\
{y_I} = \frac{1}{2}\left( {{y_A} + {y_C}} \right)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_C} = 2{x_I} - {x_A} = 3\\
{y_C} = 2{y_I} - {y_A} = 9
\end{array} \right.\)

Suy ra C(3;9).

BC là đường thẳng qua C và song song với AD nên BC có phương trình:

2(x−3)−5(y−9) = 0 ⇔ 2x−5y+39 = 0

CD là đường thẳng qua C và song song với AB nên CD có phương trình:

1(x−3)+3(y−9) = 0 ⇔ x+3y−30 = 0

Vậy hai cạnh còn lại của hình bình hành là

2x−5y+39 = 0 và x+3y−30 = 0

---

Cho phương trình

x²+y²+mx−2(m+1)y+1 = 0.     (1)

a) Với giá trị nào của m thì (1) là phương trình đường tròn?

b) Tìm tập hợp tâm của các đường tròn nói ở câu a).

Hướng dẫn giải:

Câu a:

Ta có: 2a = m, 2b = −2(m+1), c = 1

\( \Rightarrow a = \frac{m}{2},b =  - \left( {m + 1} \right),c = 1\)

(1) là đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0 \Leftrightarrow \frac{{{m^2}}}{4} + {\left( {m + 1} \right)^2} - 1 > 0\)

\( \Leftrightarrow \frac{5}{4}{m^2} + 2m > 0 \Leftrightarrow \left[ \begin{array}{l}
m <  - \frac{8}{5}\\
m > 0
\end{array} \right.\)

Câu b:

Với điều kiện \(m <  - \frac{8}{5}\) hoặc m > 0 thì (1) là phương trình đường tròn có tâm \(I\left( { - \frac{m}{2};m + 1} \right)\).

Ta có tọa độ của I:

\(\left\{ \begin{array}{l}
x =  - \frac{m}{2}\\
y = m + 1
\end{array} \right.\)

Khử m từ hoành độ và tung độ của I ta được 2x+y−1 = 0 vì \(m <  - \frac{8}{5}\) hoặc m > 0 nên \(x =  - \frac{m}{2} > \frac{4}{5}\) hoặc x < 0.

Vậy tập hợp tâm I của đường tròn là:

\(\left\{ \begin{array}{l}
2x + y - 1 = 0\\
\left[ \begin{array}{l}
x < 0\\
x > \frac{4}{5}
\end{array} \right.
\end{array} \right.\)

---

a) Biết đường tròn (C) có phương trình x²+y²+2ax+2by+c = 0. Chứng minh rằng phương tích của điểm M(x₀;y₀) đối với đường tròn (C) bằng x²₀+y²₀+2ax₀+2by₀+c.

b) Chứng minh rằng nếu hai đường tròn không đồng tâm thì tập hợp các điểm có cùng phương tích đối với hai đường tròn là một đường thẳng (gọi là trục đẳng phương của hai đường tròn).

Hướng dẫn giải:

Câu a:

Đường tròn (C) có tâm I(- a;- b), bán kính \(R = \sqrt {{a^2} + {b^2} - c} \)

Phương tích của điểm M(x₀;y₀) đối với đường tròn (C) là:

℘M/(C) = MI²−R² = (x_o+a)²+(y_o+b)²−(a²+b²−c) = x²_o+y²_o+2ax_o+2by_o+c

Câu b:

Cho hai đường tròn không đồng tâm

(C₁): x²+y²+2a₁x+2b₁y+c₁ = 0

(C₂): x²+y²+2a₂x+2b₂y+c₂ = 0

Gọi M(x₀;y₀) là điểm có cùng phương tích đối với (C₁) và (C₂) thì:

x²_o+y²_o+2a₁x_o+2b₁y_o+c₁=x²_o+y²_o+2a₂x_o+2b₂y_o+c2

⇔ 2(a₁−a₂)x_o+2(b₁−b₂)y_o+c₁−c₂ = 0   (1)

Vì (C₁) và (C₂) không đồng tâm nên a₁−a₂ và b₁−b₂ không đồng thời bằng 0 (tức (a₁−a₂)²+(b₁−b₂)² ≠ 0)

Do đó M(x₀;y₀) nằm trên đường thẳng có phương trình:

Δ: 2(a₁−a₂)x+2(b₁−b₂)y+c₁−c₂ = 0

Vậy tập hợp điểm M là đường thẳng Δ .

---

Cho hai đường tròn có phương trình x²+y²+2a₁x+2b1y+c₁ = 0 và x²+y²+2a₂x+2b₂y+c₂ = 0. Giả sử chúng cắt nhau ở hai điểm M, N. Viết phương trình đường thẳng MN. 

Hướng dẫn giải:

Hai đường tròn cắt nhau tại M, N thì trục đẳng phương của chùng chính là đường thẳng MN.

Áp dụng bài 7 thì MN có phương trình là

MN: 2(a₁−a₂)x+2(b₁−b₂)y+c₁−c₂ = 0

---

Cho đường tròn (C): x²+y² = 4 và điểm A(-2;3)

a) Viết phương trình của các tiếp tuyến của (C) kể từ A.

b) Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.

Hướng dẫn giải:

 

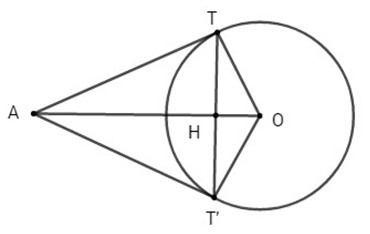
Đường tròn (C) có tâm O(0;0), bán kính R = 2.

Câu a:

Đường thẳng Δ qua A có dạng: 

a(x+2)+b(y−3) = 0 ⇔ ax+by+2a−3b = 0

Δ là tiếp tuyến của (C) \( \Leftrightarrow d\left( {O;\Delta } \right) = R\)

\(\begin{array}{l}
 \Leftrightarrow \frac{{\left| {2a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\\
 \Leftrightarrow {\left( {2a - 3b} \right)^2} = 4\left( {{a^2} + {b^2}} \right)\\
 \Leftrightarrow 5{b^2} - 12ab = 0\\
 \Leftrightarrow b\left( {5b - 12a} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
b = 0\\
12a = 5b
\end{array} \right.
\end{array}\)

Với b = 0, chọn a = 1 ta có tiếp tuyến Δ₁: x+2 = 0

Với 12a = 5b, chọn a = 5, b = 12 ta có tiếp tuyến Δ₂: 5x+12y−26 = 0

Câu b:

Gọi T, T’ là tiếp điểm của Δ₁, Δ₂ với (C) . Ta có:

\(AT = AT' = \sqrt {A{O^2} - {R^2}}  = \sqrt {13 - 4}  = 3\)

Gọi H là giao điểm của TT’ và AO, TH là đường cao của tam giác vuông ATO, ta có:

\(\begin{array}{l}
\frac{1}{{T{H^2}}} = \frac{1}{{A{T^2}}} + \frac{1}{{T{O^2}}} = \frac{1}{9} + \frac{1}{4} = \frac{{13}}{{36}}\\
 \Rightarrow TH = \frac{6}{{\sqrt {13} }} \Rightarrow TT' = 2TH = \frac{{12}}{{\sqrt {13} }}
\end{array}\)

---

Cho \(\left( E \right):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) và hypebol \(\left( H \right):\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1\).

a) Tìm tọa độ các tiêu điểm của (E) và (H).

b) Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.

c) Tìm tọa độ các giao điểm của (E) và (H).

Hướng dẫn giải:

Câu a:

Với \(\left( E \right):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) ta có: \(a = \sqrt 5 ,b = 2 \Rightarrow c = \sqrt {{a^2} - {b^2}}  = 1\)

Tọa độ các tiêu điểm của (E) là F₁(−1;0), F₂(1;0)

Với \(\left( H \right):\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1\), ta có: \(a = \sqrt 5 ,b = 2 \Rightarrow c = \sqrt {{a^2} + {b^2}}  = 3\)

Tọa độ các tiêu điểm của (H) là F₁(−3;0), F₂(3;0)

Câu b:

Vẽ (E) và (H).

 

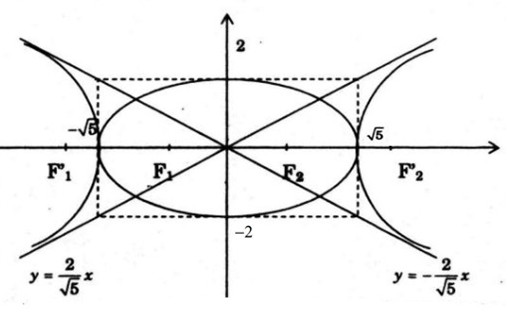
Câu c:

Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình

\(\left\{ \begin{array}{l}
\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\\
\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x^2} = 5\\
{y^2} = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x =  \pm \sqrt 5 \\
y = 0
\end{array} \right.\) 

Vậy tọa đô giao điểm của (E) và (H) là \(\left( {\sqrt 5 ;0} \right)\) và \(\left( {-\sqrt 5 ;0} \right)\).

---

Cho đường thẳng Δ: 2x−y−m = 0 và elip \(\left( E \right):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\).

a) Với giá trị nào của m thì Δ cắt (E) tại hai điểm phân biệt?

b) Với giá trị nào của m thì Δ cắt (E) tại một điểm duy nhất?

Hướng dẫn giải:

Tọa độ giao điểm của Δ và (E) là nghiệm của hệ:

\(\left\{ \begin{array}{l}
2x - y - m = 0\\
\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 2x - m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\
\frac{{{x^2}}}{5} + \frac{{{{\left( {2x - m} \right)}^2}}}{4} = 1\,\,\left( 2 \right)
\end{array} \right.\)

Ta có (2) ⇔ 4x²+5(4x²−4mx+m²) = 20

⇔ 24x²−20mx+5m²−20 = 0     (∗)

Câu a:

Δ cắt (E) tại hai điểm phân biệt

⇔ (*) có hai nghiệm phân biệt

⇔ Δ′ = 100m²−24(5m²−20) > 0

⇔−20m²+480 > 0

\(\begin{array}{l}
 \Leftrightarrow \left| m \right| < 2\sqrt 6 \\
 \Leftrightarrow  - 2\sqrt 6  < m < 2\sqrt 6 
\end{array}\)

Câu b:

Δ cắt (E) tại một điểm duy nhất ⇔ \(m =  \pm 2\sqrt 6 \)

---

Cho elip \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\).

a) Xác định tọa độ hai tiêu điểm và các đỉnh của (E).

b) Viết phương trình chính tắc của hypebol (H) nhận các tiêu điểm của (E) làm đỉnh và có hai tiêu điểm là hai đỉnh của elip (E).

c) Vẽ phác elip (E) và hypebol (H) nói ở câu b) trong cùng một hệ trục tọa độ.

d) Viết phương trình của đường tròn đi qua các giao điểm của hai đường cônic nói trên.

Hướng dẫn giải:

Câu a:

Ta có: \(a = 5,b = 3,c = \sqrt {{a^2} - {b^2}}  = 4\)

Tọa độ các tiêu điểm của (E) là F₁(−4;0), F₂(4;0)

Tọa độ các đỉnh của (E) là A₁(−5;0), A₂(5;0), B₁(0;−3), B₂(0;3)

Câu b:

(H) nhận (-4;0) và (4;0) làm đỉnh thì a = 4

(H) nhận (-5;0) và (5;0) làm tiêu điểm thì có c = 5

⇒ b² = c²−a² = 25−16 = 9 ⇒ b = 3

Vậy phương trình chính tắc của hypebol (H) là : \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)

Câu c:

Vẽ (E) và (H).

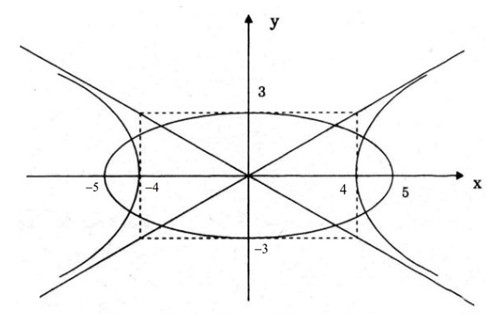
Câu d:

Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}
\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\\
\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x^2} = \frac{{800}}{{41}}\\
{y^2} = \frac{{81}}{{41}}
\end{array} \right.\)

Vậy (E) và (H) cắt nhau tại 4 điểm có tọa độ thỏa phương trình \({x^2} + {y^2} = \frac{{881}}{{41}}\)

Vậy đường tròn đi qua các giao điểm của (E) và (H) có phương trình là \({x^2} + {y^2} = \frac{{881}}{{41}}\)

---

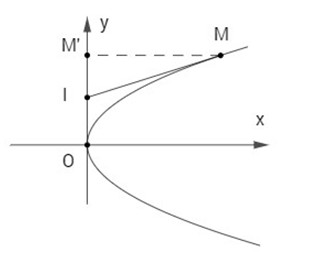
Cho parabol (P): y² = 2px. Với mỗi điểm M trên (P) (M khác O), gọi M’ là hình chiếu của M trên Oy và I  là trung điểm của đoạn OM’. Chứng minh rằng đường thẳng IM cắt parabol đã cho tại một điểm duy nhất. 

Hướng dẫn giải:

 

Giả sử M(x_o;y_o) ∈ (P) ta có y²_o = 2px_o (x_o ≠ 0) . M’ là hình chiếu của M trên Oy nên M′(0;y_o), khi đó \(I\left( {0;\frac{{{y_0}}}{2}} \right) \Rightarrow \overrightarrow {IM}  = \left( {{x_0};\frac{{{y_0}}}{2}} \right)\) là vectơ chỉ phương của đường thẳng IM.

Phương trình tham số của IM là:

\(\left\{ \begin{array}{l}
x = {x_0}t\\
y = \frac{{{y_0}}}{2} + \frac{{{y_0}}}{2}t
\end{array} \right.\)

Thay x, y trong phương trình tham số của IM vào phương trình của (P) ta được:

\(\frac{{y_0^2}}{4}\left( {1 + {t^2}} \right) = 2p{x_0}t\)

mà 2px_o=y²_o nên y²_o(1+t²) = 4y²_ot ⇔ (1+t²) = 4t ( do y_o ≠ 0) 

⇔ (t−1)² = 0 ⇔ t = 1                                                 

Vậy IM cắt (P) tại điểm duy nhất M(x_o;y_o).

---

Cho parabol (P): \({y^2} = \frac{1}{2}x\). Gọi M,N là hai điểm di động trên (P) sao cho OM⊥ON (M,N không trùng với O). Chứng minh rằng đường thẳng MN luôn đi qua một điểm cố định.

Hướng dẫn giải:

Giả sử M(2y²₁;y₁) ∈ (P), N(2y²₂;y₂) ∈ (P) trong đó y₁,y₂ ≠ 0 và y₁ ≠ y₂, vì \(\overrightarrow {OM} .\overrightarrow {ON}  = 0\) nên \(4y_1^2y_2^2 + {y_1}{y_2} = 0\)

Suy ra 4y₁y₂+1 = 0 ⇔ \({y_1}{y_2} =  - \frac{1}{4}\)

Ta có \(\overrightarrow {MN}  = \left( {2y_2^2 - 2y_1^2;{y_2} - {y_1}} \right) = \left( {{y_2} - {y_1}} \right).\left( {2{y_2} + 2{y_1};1} \right)\)

Vì y₁ ≠ y₂ nên vec tơ chỉ phương của đường thẳng MN là (2y₁+2y₂;1)

Do đó vec tơ pháp tuyến của MN là \(\overrightarrow n  = \left( {1; - 2{y_1} - 2{y_2}} \right)\)

Phương trình tổng quát của MN là:

1.(x−2y²₁)−(2y₁+2y₂).(y−y₁) = 0

Tìm giao điểm của MN với trục hoành bằng cách thay y = 0 vào (*) ta được

\(x - 2y_1^2 + 2y_2^2 + 2{y_1}{y_2} = 0 \Leftrightarrow x = \frac{1}{2}\)

Vậy MN đi qua điểm \(\left( {\frac{1}{2};0} \right)\) cố định.

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Ôn tập Chương 3 Phương pháp tọa độ trong mặt phẳng với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.