Mời các em học sinh lớp 10 cùng tham khảo tài liệu Hướng dẫn giải chi tiết bài tập SGK Toán 10 nâng cao Ôn tập Chương 3 do HỌC247 tổng hợp và biên soạn dưới đây. Nội dung tài liệu bao gồm phương pháp giải và đáp án gợi ý được trình bày một cách khoa học và dễ hiểu, giúp các em dễ dàng vận dụng, nâng cao kỹ năng làm bài. Chúc các em học tốt!
Bài 50 trang 101 SGK Toán 10 nâng cao
Bài 51 trang 101 SGK Toán 10 nâng cao
Bài 52 trang 101 SGK Toán 10 nâng cao
Bài 53 trang 101 SGK Toán 10 nâng cao
Bài 54 trang 101 SGK Toán 10 nâng cao
Bài 55 trang 101 SGK Toán 10 nâng cao
Bài 56 trang 101 SGK Toán 10 nâng cao
Bài 57 trang 101 SGK Toán 10 nâng cao
Bài 58 trang 102 SGK Toán 10 nâng cao
Bài 59 trang 102 SGK Toán 10 nâng cao
Bài 60 trang 102 SGK Toán 10 nâng cao
Bài 61 trang 102 SGK Toán 10 nâng cao
Bài 62 trang 102 SGK Toán 10 nâng cao
Bài 50 trang 101 SGK Toán 10 nâng cao
Phương trình ax + b = 0 có thể có nghiệm trong những trường hợp nào?
Hướng dẫn giải:
- Nếu a ≠ 0 thì phương trình có nghiệm duy nhất
- Nếu a = 0, b = 0 thì phương trình có vô số nghiệm
Vậy phương trình có nghiệm khi a ≠ 0 hoặc a = b = 0
Bài 51 trang 101 SGK Toán 10 nâng cao
Giả sử ba phương trình f(x).g(x) = 0, f(x) = 0 và g(x) = 0 (với cùng tập xác định) có các tập nghiệm lần lượt là T, T1 và T2. Hãy chọn kết luận đúng trong hai kết luận sau:
a) S = S1 ∩ S2;
b) S = S1 ∪ S2.
Hướng dẫn giải:
Ta có:
Chọn b) S = S1∪ S2
Bài 52 trang 101 SGK Toán 10 nâng cao
Hệ phương trình dạng ( và ) có thể có nghiệm trong trường hợp nào ?
Áp dụng: Tìm a để hệ phương trình có nghiệm ?
Hướng dẫn giải:
Hệ đã cho có nghiệm khi D ≠ 0 hoặc D = Dx = Dy = 0
Áp dụng:
Ta có:
- Nếu a ≠ ±1 hệ có nghiệm duy nhất
- Nếu a = 1 thì hệ có vô số nghiệm
- Nếu a = −1 thì hệ vô nghiệm (Do Dx = - 2 ≠ 0)
Vậy hệ có nghiệm ⇔ a ≠ −1
Bài 53 trang 101 SGK Toán 10 nâng cao
Biết rằng phương trình ax2 + bx + c = 0 có một nghiệm kép xo. Hãy chọn mệnh đề đúng trong các mệnh đề sau:
(A) Tam thức bậc hai ax2 + bx + c có thể viết dưới dạng bình phương của một nhị thức bậc nhất;
(B) Parabol y = ax2 + bx + c có đỉnh thuộc trục hoành;
(C) Phương trình cx2 + bx + a = 0 cũng có một nghiệm kép là
Hướng dẫn giải:
Chọn (B): (P) có đỉnh thuộc trục hoành
Chú ý (A) chỉ đúng nếu a > 0
(C) chỉ đúng nếu c ≠ 0
Bài 54 trang 101 SGK Toán 10 nâng cao
Giải và biện luận phương trình: m(mx –1) = x + 1
Hướng dẫn giải:
Ta có:
m(mx –1) = x + 1 ⇔ (m2–1)x = m + 1
- Nếu m ≠ ± 1 thì phương trình có nghiệm:
- Nếu m = 1 thì (1) thành 0x = 2; S = Ø
- Nếu m = −1 thì (1) thành 0x = 0; S = R
Bài 55 trang 101 SGK Toán 10 nâng cao
Cho phương trình p(x + 1) − 2x = p2 + p − 4. Tìm các giá trị của p để:
a) Phương trình nhận 1 làm nghiệm;
b) Phương trình có nghiệm;
c) Phương trình vô nghiệm.
Hướng dẫn giải:
Câu a:
x = 1 là nghiệm phương trình:
⇔ 2p − 2 = p2 + p − 4 ⇔ p2 − p − 2 = 0
Câu b:
Ta có: p(x + 1) – 2x = p2 + p – 4 ⇔ (p – 2)x = p2 – 4
- Nếu p ≠ 2: phương trình có nghiệm x = p + 2
- Nếu p = 2: phương trình có vô số nghiệm
Vậy với mọi p, phương trình luôn có nghiệm
Câu c:
Theo b) ta thấy: không có p nào thỏa mãn để phương trình vô nghiệm.
Bài 56 trang 101 SGK Toán 10 nâng cao
Ba cạnh của một tam giác vuông có độ dài là 3 số tự nhiên liên tiếp. Tính độ dài của chúng.
Hướng dẫn giải:
Gọi độ dài ngắn nhất là x (điều kiện x nguyên dương)
Theo giả thiết, độ dài của hai cạnh kia là x + 1 và x + 2, trong đó cạnh huyền dài x + 2
Theo định lý Py-ta-go, ta có phương trình:
+ (x + 1)2 = (x + 2)2
Phương trình này tương đương với:
Vậy độ dài của các cạnh của tam giác vuông là 3, 4 và 5.
Bài 57 trang 101 SGK Toán 10 nâng cao
Cho phương trình (m − 1)x2 + 2x − 1 = 0
a) Giải và biện luận phương trình.
b) Tìm các giá trị của m sao cho phương trình có hai nghiệm khác dấu.
c) Tìm các giá trị của m sao cho tổng bình phương hai nghiệm của nó bằng 1.
Hướng dẫn giải:
Câu a:
- Với m = − 1, phương trình có nghiệm là
- Với m ≠ 1, ta có: Δ′ = 1 + m – 1 = m
- Với m < 0: S = Ø
- Với m = 0: S = {1}
- Với m > 0:
Câu b:
Phương trình có hai nghiệm trái dấu
Câu c:
Điều kiện để phương trình có hai nghiệm: 1 ≠ m > 0
Theo định lý Vi-ét:
Ta có:
Bài 58 trang 102 SGK Toán 10 nâng cao
Với giá trị nào của a thì hai phương trình sau có nghiệm chung:
x2 + x + a = 0 và x2 + ax + 1 = 0
Hướng dẫn giải:
Giả sử x0 là nghiệm chung của hai phương trình, ta có:
x02 + x0 + a = 0 (1)
x02 + ax0 + 1 = 0 (2)
Lấy (1) trừ (2) ta có:
(1 − a)x0 + a − 1 = 0 ⇔ (1 − a)(x0 − 1) = 0
- Với x0 = 1 ⇒ a = −2
- Với a = 1 thì x02 + x0 + 1 = 0 (vô nghiệm)
- Với a = − 2 hai phương trình x2 + x − 2 = 0 và x2 − 2x + 1 = 0 có nghiệm chung là x = 1
Vậy a = −2
Bài 59 trang 102 SGK Toán 10 nâng cao
Cho các phương trình:
x2 + 3x − m + 1 = 0 (1) và 2x2 − x + 1 − 2p = 0 (2)
a) Biện luận số nghiệm của mỗi phương trình bằng đồ thị.
b) Kiểm tra lại kết quả trên bằng phép tính.
Hướng dẫn giải:
Câu a:
* Xét phương trình x2 + 3x − m + 1 = 0
Ta có: (1) ⇔ x2 + 3x + 1 = m
Gọi (d) là đường thẳng y = m
Đồ thị hàm số y = x2 + 3x + 1 là parabol (P) có đỉnh là điểm (−1,5;−1,25) và hướng bề lõm lên trên.
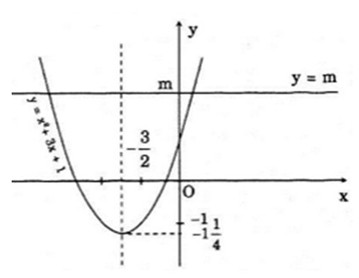
Do đó:
- Khi m < −1,25 thì (d) không cắt (P), phương trình vô nghiệm.
- Khi m = −1,25 thì (d) và (P) có một điểm chung, phương trình có một nghiệm.
- Khi m > −1,25 thì (d) cắt (P) tại hai điểm. Phương trình có hai nghiệm phân biệt.
* Xét phương trình 2x2 − x + 1 – 2p = 0 (2)
(2) ⇔ 2x2 – x + 1 = 2p
Gọi (d) là đường thẳng y = 2p; (P) là parabol y = 2x2 – x + 1
Parabol (P) có đỉnh tại điểm và hướng bề lõm lên trên.
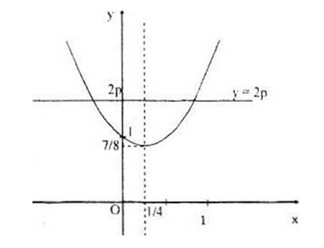
Do đó:
- Nếu , tức là thì (d) không cắt (P), phương trình vô nghiệm.
- Nếu , tức là thì (d) và (P) có một điểm chung, phương trình có một nghiệm.
- Nếu , tức là thì (d) cắt (P) tại hai điểm chung, phương trình có hai nghiệm.
Câu b:
* Xét phương trình (1) có : Δ1 = 9 + 4m – 4 = 4m + 5
- Nếu thì (1) vô nghiệm
- Nếu thì (1) có nghiệm kép
- Nếu thì (1) có hai nghiệm phân biệt
Rõ ràng kết quả biện luận bằng đồ thị số nghiệm của (1) và kết quả biện luận số nghiệm của (1) bằng phép tính là như nhau.
* Xét phương trình :
2x2 – x + 1 – 2p = 0, có Δ2 = 1 – 8 + 16p = 16p - 7
- Nếu thì (2) vô nghiệm
- Nếu thì (2) có nghiệm kép
- Nếu thì (2) có hai nghiệm phân biệt
Ta thấy kết quả biện luận số nghiệm bằng đồ thị và kết quả biện luận số nghiệm của (2) bằng phép tính là như nhau.
Bài 60 trang 102 SGK Toán 10 nâng cao
Giải các hệ phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Đặt S = x + y; P = xy ta có:
- Với S = 3, P = 2 thì x, y là nghiệm của phương trình:
- Với S = - 3, P = 2 thì x, y là nghiệm của phương trình:
Câu b:
Đặt S = x + y, P = xy ta có:
- Với S = 0, P = - 1 thì x, y là nghiệm phương trình:
Do đó ta có nghiệm (1;- 1), (- 1;1)
- Với thì x, y là nghiệm của phương trình:
Vậy hệ có 6 nghiệm
Vậy hệ phương trình đã cho có 4 nghiệm (1;2), (2;1), (- 1;- 2), (- 2;- 1)
Bài 61 trang 102 SGK Toán 10 nâng cao
Giải và biện luận các hệ phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Ta có:
- Với m ≠ 3 và m ≠ 2 hệ có nghiệm duy nhất (x,y) với
- Với m = 3: hệ vô nghiệm (do Dy = 5 ≠ 0)
- Với m = −2 hệ thành
Do đó hệ có vô số nghiệm dạng
Câu b:
Ta có:
+ Với a ≠ −3 và a ≠ 7 hệ có nghiệm duy nhất (x,y) với
+ Với a = −3 hệ thành (vô nghiệm)
+ Với a = 7, hệ thành
Hệ có vô số nghiệm dạng
Bài 62 trang 102 SGK Toán 10 nâng cao
Giải và biện luận các hệ phương trình
a)
b)
Hướng dẫn giải:
Câu a:
Theo định lý Vi-ét đảo, x và y là nghiệm của hệ phương trình:
X2 – 4X + m = 0 (1)
Ta có: Δ’ = 4 – m
Do đó:
+ Nếu m > 4 thì Δ’ < 0 thì phương trình (1) vô nghiệm nên hệ đã cho vô nghiệm
+ Nếu m = 4 thì Δ’ = 0 thì phương trình (1) có một nghiệm kép X = 2 nên hệ đã cho có một nghiệm duy nhất (x,y) = (2,2)
+ Nếu m < 4 thì Δ’ > 0 thì phương trình (1) có hai nghiệm phân biệt nên hệ đã cho có hai nghiệm:
Câu b:
Ta có:
Xét riêng phương trình 4x2 + (3x – 1)2 = 4m ⇔ 13x2 – 6x – 4m + 1= 0 (2)
Phương trình (2) có biệt thức thu gọn Δ’ = 4(13m – 1).
Do đó:
+ Nếu , phương trình (2) vô nghiệm nên hệ vô nghiệm.
+ Nếu , phương trình (2) có một nghiệm nên hệ có nghiệm là
+ Nếu thì phương trình (2) có hai nghiệm phân biệt nên hệ có hai nghiệm:
Bài 63 trang 102 SGK Toán 10 nâng cao
Tìm a, b và c để Parabol y = ax2 + bx + c (P) có đỉnh là I(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.
Hướng dẫn giải:
Ta có I(1;- 4) là đỉnh của (P) nên:
Ta có hệ phương trình:
Vậy (P): y = x2 - 2x - 3
Đồ thị (P):
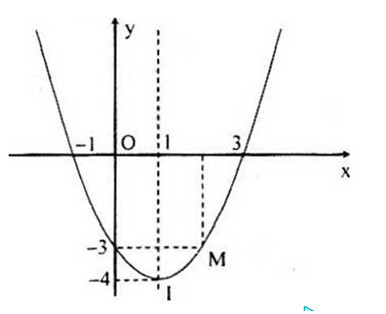
Bài 64 trang 102 SGK Toán 10 nâng cao
Cho tam giác ABC có BC = a; AC = b; AB = c.Ta lấy một điểm M trên cạnh BC. Qua M, ta kẻ các đường thẳng ME và MF thứ tự song song với các cạnh AC và AB (E ∈ AB, F ∈ AC). Hỏi phải lấy điểm M cách B bao nhiêu để tổng ME + MF = l (l là độ dài cho trước)? Biện luận theo l, a, b và c
Hướng dẫn giải:
Đặc x = MB (điều kiện: 0 < x < a)
Theo định lý Ta – lét, ta có:
Điều kiện ME + MF = l cho ta phương trình:
- Nếu b = c (tức là tam giác ABC cân tại A) thì phương trình (1) vô nghiệm nếu l ≠ c; nghiệm đúng với mọi x nếu l = c. Điều này có nghĩa là:
- Khi tam giác ABC cân tại A và l ≠ AB thì không có điểm M nào trên cạnh BC thỏa mãn điều kiện của tam giác.
- Khi tam giác ABC cân tại A và l = ABthì mọi điểm M nằm trên cạnh BC đều thỏa mãn điều kiện của tam giác.
- Nếu b ≠ c (tức là tam giác ABC không cân ở A), thì phương trình (1) có một nghiệm duy nhất
Xét điều kiện 0 < x < a:
Với b ≠ c nên có hai trường hợp:
+ Với b > c, ta có:
+ Với b < c, ta có:
Hai kết quả trên có nghĩa là giá trị là nghiệm của bài toán (điểm M cách B một khoảng bằng khi và chỉ độ dài l nằm giữa các độ dài b và c)
Tư liệu nổi bật tuần
- Xem thêm







