Dưới đây là Hướng dẫn giải bài tập Toán 10 nâng cao Chương 6 Luyện tập (trang 206, 207) được hoc247 biên soạn và tổng hợp, nội dung bám sát theo chương trình SGK Đại số 10 nâng cao giúp các em học sinh nắm vững phương pháp giải bài tập và ôn tập kiến thức hiệu quả hơn.
Bài 30 trang 206 SGK Toán 10 nâng cao
Hỏi các góc lượng giác có cùng tia đầu và có số đo như sau: 2594o; -646o; -2446o và 74o thì có cùng tia cuối không?
Hướng dẫn giải:
Ta có:
25940 = 740 + 7.3600
- 6460 = 740 – 2.3600
- 22460 = 740 - 7.3600
Do đó, các góc lượng giác trên có cùng tia cuối.
Bài 31 trang 206 SGK Toán 10 nâng cao
Xác định dấu của các giá trị lượng giác sau:
\(\cos {250^0};\tan \left( { - {{672}^0}} \right);\tan \frac{{31\pi }}{8};\sin \left( { - {{1050}^0}} \right);\cos \frac{{16\pi }}{5}\)
Hướng dẫn giải:
Do 1800 < 2500 < 2700 nên cos 2500 < 0
\(\begin{array}{l}
\tan \left( { - {{672}^0}} \right) = - \tan {672^0} = - \tan \left( { - {{48}^0} + {{2.360}^0}} \right) = \tan {48^0} > 0\\
\tan \frac{{31\pi }}{8} = \tan \left( { - \frac{\pi }{8} + 4\pi } \right) = \tan \left( { - \frac{\pi }{8}} \right) = - \tan \frac{\pi }{8} < 0\\
\sin \left( { - {{1050}^0}} \right) = \sin \left( {{{30}^0} - {{3.360}^0}} \right) = \sin {30^0} = \frac{1}{2} > 0\\
\cos \frac{{16\pi }}{5} = \cos \left( {3\pi - \frac{\pi }{5}} \right) = - \cos \frac{\pi }{5} < 0
\end{array}\)
Bài 32 trang 206 SGK Toán 10 nâng cao
Hãy tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:
a) \(\sin \alpha = \frac{4}{5};\cos \alpha < 0\)
b) \(\cos \alpha = - \frac{8}{{17}};\frac{\pi }{2} < \alpha < \pi \)
c) \(\tan \alpha = \sqrt 3 ;\pi < \alpha < \frac{{3\pi }}{2}\)
Hướng dẫn giải:
Câu a:
Vì \(\cos \alpha < 0\) nên ta có:
\(\begin{array}{l}
\cos \alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \sqrt {1 - \frac{{16}}{{25}}} = - \frac{3}{5}\\
\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \frac{4}{3}\\
\cot \alpha = \frac{1}{{\tan \alpha }} = - \frac{3}{4}
\end{array}\)
Câu b:
Vì \(\frac{\pi }{2} < \alpha < \pi \Rightarrow \sin \alpha > 0\) nên:
\(\begin{array}{l}
\Rightarrow \sin \alpha = \sqrt {1 - {{\cos }^2}\alpha } = \sqrt {1 - {{\left( {\frac{8}{{17}}} \right)}^2}} = \frac{{15}}{{17}}\\
\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \frac{{15}}{8}\\
\cot \alpha = \frac{1}{{\tan \alpha }} = - \frac{8}{{15}}
\end{array}\)
Câu c:
Vì \(\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \cos \alpha < 0\) nên:
\(\begin{array}{l}
\Rightarrow \cos \alpha = \frac{{ - 1}}{{\sqrt {1 + {{\tan }^2}\alpha } }} = - \frac{1}{{\sqrt {1 + {{\left( {\sqrt 3 } \right)}^2}} }} = - \frac{1}{2}\\
\sin \alpha = \tan \alpha .\cos \alpha - \frac{{\sqrt 3 }}{2}\\
\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{{\sqrt 3 }}{3}
\end{array}\)
Bài 33 trang 206 SGK Toán 10 nâng cao
Tính
a) Tính \(\sin \frac{{25\pi }}{6} + \cos \frac{{25\pi }}{3} + \tan \left( { - \frac{{25\pi }}{4}} \right)\)
b) Biết \(\sin \left( {\pi + \alpha } \right) = - \frac{1}{3}\), hãy tính \(\cos \left( {2\pi - \alpha } \right)\), \(\tan \left( {\alpha - 7\pi } \right)\) và \(\sin \left( {\frac{{3\pi }}{2} - \alpha } \right)\)
Hướng dẫn giải:
Câu a:
\(\begin{array}{l}
\sin \frac{{25\pi }}{6} = \sin \left( {4\pi + \frac{\pi }{6}} \right) = \sin \frac{\pi }{6} = \frac{1}{2}\\
\cos \frac{{25\pi }}{3} = \cos \left( {8\pi + \frac{\pi }{3}} \right) = \cos \frac{\pi }{3} = \frac{1}{2}\\
\tan \left( { - \frac{{25\pi }}{4}} \right) = - \tan \left( {6\pi + \frac{\pi }{4}} \right) = - \tan \frac{\pi }{4} = - 1\\
\Rightarrow \sin \frac{{25\pi }}{6} + \cos \frac{{25\pi }}{3} + \tan \left( { - \frac{{25\pi }}{4}} \right) = 0
\end{array}\)
Câu b:
\(\begin{array}{l}
\sin \left( {\pi + \alpha } \right) = - \frac{1}{3} \Rightarrow \sin \alpha = \frac{1}{3}\\
\cos \left( {2\pi - \alpha } \right) = \cos \left( { - \alpha } \right) = \cos \alpha = \pm \sqrt {1 - {{\sin }^2}\alpha } = \pm \frac{{2\sqrt 2 }}{3}\\
\tan \left( {\alpha - 7\pi } \right) = \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \pm \frac{1}{{2\sqrt 2 }}\\
\sin \left( {\frac{{3\pi }}{2} - \alpha } \right) = \sin \left( {\pi + \frac{\pi }{2} - \alpha } \right) = - \sin \left( {\frac{\pi }{2} - \alpha } \right) = - \cos \alpha = \pm \frac{{2\sqrt 2 }}{3}
\end{array}\)
Bài 34 trang 207 SGK Toán 10 nâng cao
Chứng minh rằng:
a) \(\frac{{1 - 2\sin \alpha \cos \alpha }}{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }} = \frac{{1 - \tan \alpha }}{{1 + \tan \alpha }}\)
b) \({\tan ^2}\alpha - {\sin ^2}\alpha = {\tan ^2}\alpha .{\sin ^2}\)
c) \(2\left( {1 - \sin \alpha } \right)\left( {1 + \cos \alpha } \right) = {\rm{ }}{\left( {1 - \sin \alpha + \cos \alpha } \right)^2}\)
Hướng dẫn giải:
Câu a:
\(\begin{array}{l}
\frac{{1 - 2\sin \alpha \cos \alpha }}{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }} = \frac{{{{\left( {\cos \alpha - \sin \alpha } \right)}^2}}}{{\left( {\cos \alpha - \sin \alpha } \right)\left( {\cos \alpha + \sin \alpha } \right)}}\\
= \frac{{\cos \alpha - \sin \alpha }}{{\cos \alpha + \sin \alpha }} = \frac{{\cos \alpha \left( {1 - \tan \alpha } \right)}}{{\cos \alpha \left( {1 + \tan \alpha } \right)}} = \frac{{1 - \tan \alpha }}{{1 + \tan \alpha }}
\end{array}\)
Câu b:
\({\tan ^2}\alpha - {\sin ^2}\alpha = {\tan ^2}\alpha \left( {1 - {{\cos }^2}\alpha } \right) = {\tan ^2}\alpha .{\sin ^2}\alpha \)
Câu c:
\(\begin{array}{l}
2\left( {1 - \sin \alpha } \right)\left( {1 + \cos \alpha } \right)\\
= 2 - 2\sin \alpha + 2\cos \alpha - 2\sin \alpha \cos \alpha \\
= 1 + {\sin ^2}\alpha + {\cos ^2}\alpha - 2\sin \alpha + 2\cos \alpha - 2\sin \alpha \cos \alpha \\
= {\left( {1 - \sin \alpha + \cos \alpha } \right)^2}
\end{array}\)
Bài 35 trang 207 SGK Toán 10 nâng cao
Biết \(\sin \alpha - \cos \alpha = m\), hãy tính \({\sin ^3}\alpha - {\cos ^3}\alpha \)
Hướng dẫn giải:
Ta có:
\(\begin{array}{l}
{\sin ^3}\alpha - {\cos ^3}\alpha \\
= \left( {\sin \alpha - \cos \alpha } \right)\left( {{{\sin }^2}\alpha + \sin \alpha \cos \alpha + {{\cos }^2}\alpha } \right)\\
= m\left( {1 + \sin \alpha \cos \alpha } \right)\,\,\,\,\,\left( 1 \right)
\end{array}\)
Từ \(\sin \alpha - \cos \alpha = m \Rightarrow 1 - 2\sin \alpha \cos \alpha = {m^2}\)
\( \Rightarrow \sin \alpha \cos \alpha = \frac{{1 - {m^2}}}{2}\,\,\,\,\,\,\left( 2 \right)\)
Thay (2) vào (1) ta được: \({\sin ^3}\alpha - {\cos ^3}\alpha = m\left( {1 + \frac{{1 - {m^2}}}{2}} \right) = \frac{m}{2}\left( {3 - {m^2}} \right)\)
Bài 36 trang 207 SGK Toán 10 nâng cao
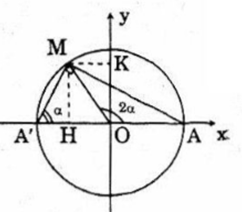
Với số \(\alpha ,\,0 < \alpha < \frac{\pi }{2}\), xét điểm M của đường tròn lượng giác xác định bởi 2α, rồi xét tam giác vuông A’MA (A’ đối xứng với A qua tâm O của đường tròn).
a) Tính AM2 bằng hai cách khác nhau để suy ra: cos2α = 1 – 2sin2α
b) Tính diện tích tam giác A’MA bằng hai cách khác nhau để suy ra: sin2α = 2sinα cosα
c) Chứng minh: \(\sin \frac{\pi }{8} = \frac{1}{2}\sqrt {2 - \sqrt 2 } ;\cos \frac{\pi }{8} = \frac{1}{2}\sqrt {2 + \sqrt 2 } \) rồi tính các giá trị lượng giác của các góc \(\frac{{3\pi }}{8}\) và \(\frac{{5\pi }}{8}\)
Hướng dẫn giải:
Câu a:
Ta có:
\(\begin{array}{l}
A{M^2} = \overline {AH} .\overline {AA'} = \left( {\overline {AO} + \overline {OH} } \right).\overline {AA'} \\
= \left( { - 1 + \cos 2\alpha } \right).\left( { - 2} \right) = 2\left( {1 - \cos 2\alpha } \right)
\end{array}\)
Ta lại có: \(A{M^2} = AA{'^2}.{\sin ^2}\alpha = 4{\sin ^2}\alpha \Rightarrow 2{\sin ^2}\alpha = 1 - \cos 2\alpha \)
Câu b:
Ta có: \({S_{A'MA}} = \frac{1}{2}AA'.MH = MH = \sin 2\alpha \)
Lại có: \({S_{A'MA}} = \frac{1}{2}A'M.AM = \frac{1}{2}A'A.\cos \alpha .A'A.\sin \alpha = 2\sin \alpha \cos \alpha \)
Vậy \(\sin 2\alpha = 2\sin \alpha \cos \alpha \)
Câu c:
Ta có \(\cos \frac{\pi }{4} = 1 - 2{\sin ^2}\frac{\pi }{8}\) nên:
\(\begin{array}{l}
{\sin ^2}\frac{\pi }{8} = \frac{1}{2}\left( {1 - \frac{{\sqrt 2 }}{2}} \right) = \frac{{2 - \sqrt 2 }}{4}\\
\sin \frac{\pi }{8} = \frac{{\sqrt {2 - \sqrt 2 } }}{2}\\
\cos \frac{\pi }{4} = 2{\cos ^2}\frac{\pi }{8} - 1 \Rightarrow {\cos ^2}\frac{\pi }{8} = \frac{1}{2}\left( {1 + \frac{{\sqrt 2 }}{2}} \right) = \frac{{2 + \sqrt 2 }}{4} \Rightarrow \cos \frac{\pi }{8} = \frac{{\sqrt {2 + \sqrt 2 } }}{2}
\end{array}\)
Vì \(\frac{{3\pi }}{8} = \frac{\pi }{2} - \frac{\pi }{8}\) nên \(\left\{ \begin{array}{l}
\cos \frac{{3\pi }}{8} = \sin \frac{\pi }{8} = \frac{{\sqrt {2 - \sqrt 2 } }}{2}\\
\sin \frac{{3\pi }}{8} = \cos \frac{\pi }{8} = \frac{{\sqrt {2 + \sqrt 2 } }}{2}\\
\tan \frac{{3\pi }}{8} = \cot \frac{\pi }{8} = \sqrt 2 + 1\\
\cot \frac{{3\pi }}{8} = \tan \frac{\pi }{8} = \sqrt 2 - 1
\end{array} \right.\)
Vì \(\frac{{5\pi }}{8} = \frac{\pi }{2} + \frac{\pi }{8}\) nên \(\left\{ \begin{array}{l}
\cos \frac{{5\pi }}{8} = - \sin \frac{\pi }{8} = \frac{{\sqrt {2 - \sqrt 2 } }}{2}\\
\sin \frac{{5\pi }}{8} = \cos \frac{\pi }{8} = \frac{{\sqrt {2 + \sqrt 2 } }}{2}\\
\tan \frac{{5\pi }}{8} = - \cot \frac{\pi }{8} = - \sqrt 2 - 1\\
\cot \frac{{5\pi }}{8} = - \tan \frac{\pi }{8} = 1 - \sqrt 2
\end{array} \right.\)
Bài 37 trang 207 SGK Toán 10 nâng cao
Trong hệ tọa độ vuông góc Oxy gắn với một đường tròn lượng giác, cho điểm P có tọa độ (2, - 3)
a) Chứng minh rằng điểm M sao cho \(\overrightarrow {OM} = \frac{{\overrightarrow {OP} }}{{\left| {\overrightarrow {OP} } \right|}}\) là giao điểm của tia OP với đường tròn lượng giác đó
b) Tính tọa độ điểm M và từ đó suy ra cosin, sin của góc lượng giác (Ox, OP)
Hướng dẫn giải:
Câu a:
Ta có:
\(\left\{ \begin{array}{l}
\overrightarrow {OM} \uparrow \uparrow \overrightarrow {OP} \\
\left| {\overrightarrow {OM} } \right| = \left| {\frac{{\overrightarrow {OP} }}{{\overrightarrow {OP} }}} \right| = \frac{{\left| {\overrightarrow {OP} } \right|}}{{\left| {\overrightarrow {OP} } \right|}} = 1
\end{array} \right.\)
Vậy M là giao của tia OP với đường tròn lượng giác.
Câu b:
Ta có: \(\left| {\overrightarrow {OP} } \right| = \sqrt {{2^2} + {{\left( { - 3} \right)}^2}} = \sqrt {13} \Rightarrow \overrightarrow {OM} = \left( {\frac{2}{{\sqrt {13} }}; - \frac{3}{{\sqrt {13} }}} \right)\)
Vậy \(\left\{ \begin{array}{l}
\cos \left( {Ox,OP} \right) = \frac{2}{{\sqrt {13} }}\\
\sin \left( {Ox,OP} \right) = - \frac{3}{{\sqrt {13} }}
\end{array} \right.\)
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 6 Luyện tập (trang 206, 207) với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
Tư liệu nổi bật tuần
- Xem thêm