Giải Toán 10 SGK nâng cao Chương 6 Bài 1 Góc lượng giác và cung lượng giác

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

a) Số đo của cung trong phụ thuộc vào bán kính của nó

b) Độ dài của cung tròn tỉ lệ với số đo của cung tròn

c) Độ dài của cung tròn tỉ lệ với bán kính của nó

d) Nếu Ou, Ov là hai tia đối nhau thì số đo góc lượng giác (Ou; Ov) là (2k + 1)π, k∈Z.

Hướng dẫn giải:

a) Sai

b) Đúng

c) Đúng

d) Đúng

---

Kim phút và kim giờ của đồng hồ lớn nhà bưu điện bờ hồ Hà Nội, theo thứ tự dài 1,75 m và 1,26 m. Hỏi trong 15 phút mũi kim phút vạch nên cung tròn có độ dài là bao nhiêu mét? Cũng câu hỏi đó cho mũi kin giờ.

Hướng dẫn giải:

Trong 15 phút, mũi kim phút vạch cung tròn có số đo \(\frac{\pi }{2}\) rad nên cung đó có độ dài là:

\(\frac{\pi }{2}.1,75 \approx 2,75\left( m \right)\)

Mũi kim giờ vạch cung tròn có số đo \(\frac{\pi }{{24}}\) rad nên cung đó có độ dài:

\(\frac{\pi }{{24}}.1,26 \approx 0,16\left( m \right)\)

---

Điền vào các ô trống trong bảng

Số đo độ	- 600	- 2400			31000
Số đo radian			\( - \frac{{3\pi }}{4}\)	\( - \frac{{16\pi }}{3}\)		\(\frac{{68\pi }}{5}\)

Hướng dẫn giải:

Áp dụng công thức \(\frac{\alpha }{\pi } = \frac{a}{{180}}\) (a được tính bằng độ, \(\alpha \) được tính bằng radian)

Ta có bảng sau:

Số đo độ	- 600	- 2400	- 1350	- 9600	31000	24480
Số đo radian	\( - \frac{\pi }{3}\)	\( - \frac{{4\pi }}{3}\)	\( - \frac{{3\pi }}{4}\)	\( - \frac{{16\pi }}{3}\)	\( - \frac{{155\pi }}{9}\)	\(\frac{{68\pi }}{5}\)

---

a) Đổi số đo độ của các cung tròn sau thành số đo radian (chính xác đến phần nghìn):

21^o30' và 75^o54'.

b) Đổi số đo radian của các cung tròn sau ra số đo độ: 2,5 (rad) và 2/π (rad) (có thể dùng máy tính bỏ túi).

Hướng dẫn giải:

Câu a:

Ta có:

\(\begin{array}{l}
{21^0}30' = \frac{{21,5\pi }}{{180}} \approx 0,375\left( {rad} \right)\\
{75^0}54' = \frac{{75,9\pi }}{{180}} \approx 1,325\left( {rad} \right)
\end{array}\)

Câu b:

Ta có:

\(\begin{array}{l}
2,5rad = {\left( {\frac{{2,5.180}}{\pi }} \right)^0} \approx {143^0}14'\\
\frac{2}{\pi }rad = \left( {\frac{{\frac{2}{\pi }.180}}{\pi }} \right) \approx {36^0}29'
\end{array}\)

---

Coi kim giờ của đồng hồ là tia Ou, kim phút là tia Ov. Hãy tìm số đo của góc lượng giác (Ou;Ov) khi đồng hồ chỉ 3 giờ, chỉ 4 giờ, chỉ 9 giờ , chỉ 10 giờ.

Hướng dẫn giải:

Số đo lượng giác (Ou, Ov) khi đồng hồ chỉ 3 giờ, chỉ 4 giờ, chỉ 9 giờ, chỉ 10 giờ lần lượt là:

\(\begin{array}{l}
\frac{\pi }{2} + k2\pi \left( {k \in Z} \right);\\
\frac{{2\pi }}{3} + k2\pi \left( {k \in Z} \right);\\
 - \frac{\pi }{2} + k2\pi \left( {k \in Z} \right);\\
 - \frac{\pi }{3} + k2\pi \left( {k \in Z} \right).
\end{array}\)

---

Chứng minh

a) Hai góc lượng giác có cùng tia đầu và có số đo \(\frac{{10\pi }}{3}\) và \(\frac{{22\pi }}{3}\) thì có cùng tia cuối

b) Hai góc lượng giác có cùng tia đầu và có số đo là 645^o và - 435^o thì có cùng tia cuối

Hướng dẫn giải:

Hai góc lượng giác có cùng tia đầu và tia cuối khi và chỉ khi hiệu của chính bằng 2kπ hoặc k360⁰ (k ∈ Z)

Câu a:

Ta có: \(\frac{{22\pi }}{3} - \frac{{10\pi }}{3} = 4\pi  = 2.2\pi \)

Vậy ta đã chứng minh được hai góc lượng giác có cùng tia đầu và có số đo \(\frac{{10\pi }}{3}\) và \(\frac{{22\pi }}{3}\) thì có cùng tia cuối

Câu b:

Ta có: \({645^0} - \left( { - {{435}^0}} \right) = {1080^0} = {3.360^0}\)

Vậy ta đã chứng minh được hai góc lượng giác có cùng tia đầu và có số đo là 645o và - 435o thì có cùng tia cuối

---

Tìm số đo a^o, -180^o < a ≤ 180^o của góc lượng giác có cùng tia đầu và tia cuối với góc trên mỗi hình sau:

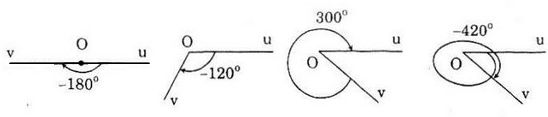
Hướng dẫn giải:

a) a⁰ = 180⁰

b) a⁰ = - 120⁰

c) a⁰ = - 60⁰

d) a⁰ = - 60⁰

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 6 Bài 1 Góc lượng giác và cung lượng giác với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.