DŲ░ß╗øi ─æ├óy l├Ā HŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp To├Īn 10 n├óng cao ChŲ░ŲĪng 4 Luyß╗ćn tß║Łp (trang 127) ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp, nß╗Öi dung b├Īm s├Īt theo chŲ░ŲĪng tr├¼nh SGK ─Éß║Īi sß╗æ 10 n├óng cao gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n tß║Łp kiß║┐n thß╗®c hiß╗ću quß║Ż hŲĪn.
B├Āi 36 trang 127 SGK To├Īn 10 n├óng cao
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc bß║źt phŲ░ŲĪng tr├¼nh:
a) mx + 4 > 2x + m2
b) 2mx + 1 Ōēź x + 4m2
c) x(m2 - 1) < m4 - 1
d) 2(m+1)x Ōēż (m+1)2(x-1)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
mx + 4 > 2x+m2 Ōćö (m - 2)x > m2 - 4 (1)
Nß║┐u m = 2, bß║źt phŲ░ŲĪng tr├¼nh trß╗¤ th├Ānh 0x > 0 n├¬n v├┤ nghiß╗ćm
Nß║┐u m > 2, th├¼ (1) Ōćö x > m + 2 hay tß║Łp nghiß╗ćm l├Ā S = (m + 2;+Ōł×)
Nß║┐u m < 2, th├¼ (1) Ōćö x < m + 2 hay tß║Łp nghiß╗ćm l├Ā S = (-Ōł×;m + 2)
Câu b:
2mx + 1 Ōēź 4m2 Ōćö x(2m+1) Ōēź (2m - 1)(2m + 1) (2)
Nß║┐u \(m = \frac{1}{2}\) th├¼ bß║źt phŲ░ŲĪng tr├¼nh trß╗¤ th├Ānh 0x Ōēź 0 n├¬n n├│ tß║Łp nghiß╗ćm l├Ā R.
Nß║┐u \(m > \frac{1}{2}\) th├¼ (2) Ōćö x Ōēź 2m + 1 hay tß║Łp nghiß╗ćm cß╗¦a n├│ l├Ā [2m + 1;+Ōł×)
Nß║┐u \(m < \frac{1}{2}\) th├¼ (2) Ōćö x Ōēż 2m+1 hay tß║Łp nghiß╗ćm cß╗¦a n├│ l├Ā (-Ōł×;2m + 1]
Câu c:
x(m2 - 1) < m4 - 1 (3)
Nß║┐u m = 1 hoß║Ęc m = - 1, bß║źt phŲ░ŲĪng tr├¼nh v├┤ nghiß╗ćm
Nß║┐u -1 < m < 1 th├¼ (3) Ōćö x > m2 + 1 hay c├│ tß║Łp nghiß╗ćm l├Ā (m2+1;+Ōł×)
Nß║┐u m < - 1 hoß║Ęc m > 1 th├¼ (3) Ōćö x < m2+1 hay c├│ tß║Łp nghiß╗ćm l├Ā (-Ōł×;m2+1)
Câu d:
2(m+1)x Ōēż (m+1)2(x-1) Ōćö x(m + 1)(m - 1) Ōēź (m+1)2 (4)
Nß║┐u m = -1, bß║źt phŲ░ŲĪng tr├¼nh c├│ nghiß╗ćm l├Ā R
Nß║┐u m = 1, bß║źt phŲ░ŲĪng tr├¼nh v├┤ nghiß╗ćm
Nß║┐u -1 < m < 1, (4) Ōćö x Ōēż \(\frac{{m + 1}}{{m - 1}}\) suy ra tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh l├Ā \(\left( { - \infty ;\frac{{m + 1}}{{m - 1}}} \right]\)
Nß║┐u m < - 1 hoß║Ęc m > 1, (4) Ōćö x Ōēź \(\frac{{m + 1}}{{m - 1}}\) suy ra tß║Łp nghiß╗ćm l├Ā \(\left[ {\frac{{m + 1}}{{m - 1}}; + \infty } \right)\)
B├Āi 37 trang 127 SGK To├Īn 10 n├óng cao
Giß║Żi c├Īc bß║źt phŲ░ŲĪng tr├¼nh
a) \(\left( { - \sqrt 3 x + 2} \right)\left( {x + 1} \right)\left( {4x - 5} \right) > 0\)
b) \(\frac{{3 - 2x}}{{\left( {3x - 1} \right)\left( {x - 4} \right)}} < 0\)
c) \(\frac{{ - 3x + 1}}{{2x + 1}} \le - 2\)
d) \(\frac{{x + 2}}{{3x + 1}} \le \frac{{x - 2}}{{2x - 1}}\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Bß║Żng x├®t dß║źu
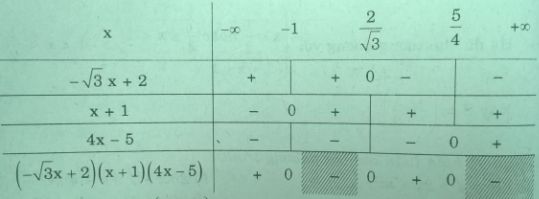
Vß║Ły tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh l├Ā \(S = \left( { - \infty ; - 1} \right) \cup \left( {\frac{2}{{\sqrt 3 }};\frac{5}{4}} \right)\)
Câu b:
Bß║Żng x├®t dß║źu

Vß║Ły tß║Łp nghiß╗ćm l├Ā \(S = \left( {\frac{1}{3};\frac{3}{2}} \right) \cup \left( {4; + \infty } \right)\)
Câu c:
Ta c├│ \(\frac{{ - 3x + 1}}{{2x + 1}} \le - 2 \Leftrightarrow \frac{{ - 3x + 1 + 2\left( {2x + 1} \right)}}{{2x + 1}} \le 0 \Leftrightarrow \frac{{x + 3}}{{2x + 1}} \le 0\)
Bß║Żng x├®t dß║źu
Vß║Ły tß║Łp nghiß╗ćm l├Ā \(S = \left[ { - 3; - \frac{1}{2}} \right)\)
Câu d:
Ta c├│
\(\begin{array}{l}
\frac{{x + 2}}{{3x + 1}} \le \frac{{x - 2}}{{2x - 1}}\\
\Leftrightarrow \frac{{\left( {x + 2} \right)\left( {2x - 1} \right) - \left( {x - 2} \right)\left( {3x + 1} \right)}}{{\left( {3x + 1} \right)\left( {2x - 1} \right)}} \le 0\\
\Leftrightarrow \frac{{ - {x^2} + 8x}}{{\left( {3x + 1} \right)\left( {2x - 1} \right)}} \le 0\\
\Leftrightarrow \frac{{x\left( {x - 8} \right)}}{{\left( {3x + 1} \right)\left( {2x - 1} \right)}} \ge 0
\end{array}\)
Bß║Żng x├®t dß║źu

Vß║Ły tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh l├Ā \(S = \left( { - \infty ; - \frac{1}{3}} \right) \cup \left[ {0;\frac{1}{2}} \right) \cup \left[ {8; + \infty } \right)\)
B├Āi 38 trang 127 SGK To├Īn 10 n├óng cao
Giß║Żi v├Ā biß╗ćn luß║Łn c├Īc bß║źt phŲ░ŲĪng tr├¼nh
a) \(\left( {2x - \sqrt 2 } \right)\left( {x - m} \right) > 0\)
b) \(\frac{{\sqrt 3 - x}}{{x - 2m + 1}} \le 0\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Ta c├│:
\(\begin{array}{l}
2x - \sqrt 2 = 0 \Leftrightarrow x = \frac{{\sqrt 2 }}{2}\\
x - m = 0 \Leftrightarrow x = m
\end{array}\)
Vß╗øi \(m < \frac{{\sqrt 2 }}{2}\), ta c├│ bß║Żng x├®t dß║źu:
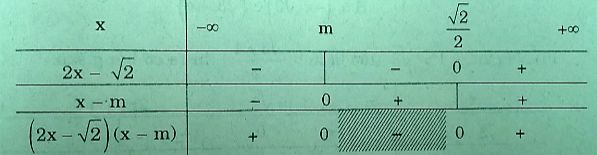
Suy ra \(S = \left( { - \infty ;m} \right) \cup \left( {\frac{{\sqrt 2 }}{2}; + \infty } \right)\)
Vß╗øi \(m = \frac{{\sqrt 2 }}{2}\) bß║źt phŲ░ŲĪng tr├¼nh trß╗¤ th├Ānh:
\(\left( {2x - \sqrt 2 } \right)\left( {x - \frac{{\sqrt 2 }}{2}} \right) > 0 \Leftrightarrow {\left( {2x - \sqrt 2 } \right)^2} > 0 \Leftrightarrow x \ne \frac{{\sqrt 2 }}{2}\)
Suy ra \(S = R\backslash \left\{ {\frac{{\sqrt 2 }}{2}} \right\}\)
Vß╗øi \(m > \frac{{\sqrt 2 }}{2}\), ta c├│ bß║Żng x├®t dß║źu:
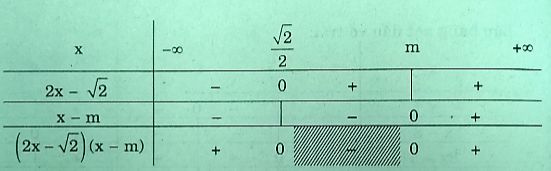
Suy ra \(S = \left( { - \infty ;\frac{{\sqrt 2 }}{2}} \right) \cup \left( {m; + \infty } \right)\)
Câu b:
Ta c├│:
\(\begin{array}{l}
\sqrt 3 - x = 0 \Leftrightarrow x = \sqrt 3 \\
x - 2m + 1 = 0 \Leftrightarrow x = 2m - 1
\end{array}\)
Vß╗øi \(2m - 1 < \sqrt 3 \Leftrightarrow m < \frac{{\sqrt 3 + 1}}{2}\), ta c├│ bß║Żng x├®t dß║źu:

Suy ra \(S = \left( { - \infty ;2m - 1} \right) \cup \left[ {\sqrt 3 ; + \infty } \right)\)
Vß╗øi \(2m - 1 = \sqrt 3 \Leftrightarrow m = \frac{{\sqrt 3 + 1}}{2}\), bß║źt phŲ░ŲĪng tr├¼nh trß╗¤ th├Ānh:
\(\frac{{\sqrt 3 - x}}{{x - \sqrt 3 }} \le 0\)
Bß║Żng x├®t dß║źu
Vß╗øi \(2m - 1 > \sqrt 3 \Leftrightarrow m > \frac{{\sqrt 3 + 1}}{2}\), ta c├│ bß║Żng x├®t dß║źu:
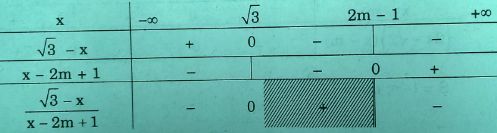
Vß║Ły tß║Łp nghiß╗ćm l├Ā \(S = \left( { - \infty ;\sqrt 3 } \right) \cup \left( {2m - 1; + \infty } \right)\)
B├Āi 39 trang 127 SGK To├Īn 10 n├óng cao
T├¼m nghiß╗ćm nguy├¬n cß╗¦a mß╗Śi hß╗ć bß║źt phŲ░ŲĪng tr├¼nh sau:
a) \(\left\{ \begin{array}{l}
6x + \frac{5}{7} > 4x + 7\\
\frac{{8x + 3}}{2} < 2x + 25
\end{array} \right.\)
b) \(\left\{ \begin{array}{l}
15x - 2 > 2x + \frac{1}{3}\\
2\left( {x - 4} \right) < \frac{{3x - 14}}{2}
\end{array} \right.\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
\(\begin{array}{l}
\left\{ \begin{array}{l}
6x + \frac{5}{7} > 4x + 7\\
\frac{{8x + 3}}{2} < 2x + 25
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
42x + 5 < 28x + 49\\
8x + 3 < 4x + 50
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
14x > 44\\
4x < 47
\end{array} \right. \Leftrightarrow \frac{{44}}{{14}} < x < \frac{{47}}{4}
\end{array}\)
V├¼ x Ōłł Z n├¬n x Ōłł {4, 5, 6, 7, 8, 9, 10, 11}
Vß║Ły tß║Łp nghiß╗ćm cß╗¦a hß╗ć l├Ā : {4, 5, 6, 7, 8, 9, 10, 11}
Câu b:
\(\begin{array}{l}
\left\{ \begin{array}{l}
15x - 2 > 2x + \frac{1}{3}\\
2\left( {x - 4} \right) < \frac{{3x - 14}}{2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
45x - 6 > 6x + 1\\
4x - 16 < 3x - 14
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
39x > 7\\
x < 2
\end{array} \right. \Leftrightarrow \frac{7}{{39}} < x < 2
\end{array}\)
V├¼ x Ōłł Z n├¬n x = 1
Vß║Ły tß║Łp nghiß╗ćm cß╗¦a hß╗ć l├Ā {1}
B├Āi 40 trang 127 SGK To├Īn 10 n├óng cao
Giß║Żi phŲ░ŲĪng tr├¼nh v├Ā bß║źt phŲ░ŲĪng tr├¼nh
a) \(\left| {x + 1} \right| + \left| {x - 1} \right| =4\,\,\, (1) \)
b) \(\frac{{\left| {2x - 1} \right|}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} > \frac{1}{2}\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Bß║Żng x├®t dß║źu
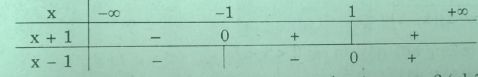
Vß╗øi x < - 1, ta c├│ \(\left( 1 \right) \Leftrightarrow - x - 1 - x + 1 = 4 \Leftrightarrow x = - 2\) (nhß║Łn)
Vß╗øi \( - 1 \le x \le 1\), ta c├│ \(\left( 1 \right) \Leftrightarrow x + 1 - x + 1 = 4 \Leftrightarrow 0x = 2\) (v├┤ nghiß╗ćm)
Vß╗øi x > 1, ta c├│ \(\left( 1 \right) \Leftrightarrow x + 1 + x - 1 = 4 \Leftrightarrow x = 2\) (nhß║Łn)
Vß║Ły S = {- 2;2}
Câu b:
Nß║┐u th├¼ bß║źt phŲ░ŲĪng tr├¼nh trß╗¤ th├Ānh:
\(\begin{array}{l}
\frac{{ - 2x + 1}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} > \frac{1}{2}\\
\Leftrightarrow \frac{{2\left( { - 2x + 1} \right) - \left( {x + 1} \right)\left( {x - 2} \right)}}{{2\left( {x + 1} \right)\left( {x - 2} \right)}} > 0\\
\Leftrightarrow \frac{{ - {x^2} - 3x + 4}}{{2\left( {x + 1} \right)\left( {x - 2} \right)}} > 0\\
\Leftrightarrow \frac{{\left( {x - 1} \right)\left( {x + 4} \right)}}{{2\left( {x + 1} \right)\left( {x - 2} \right)}} < 0
\end{array}\)
Bß║Żng x├®t dß║źu
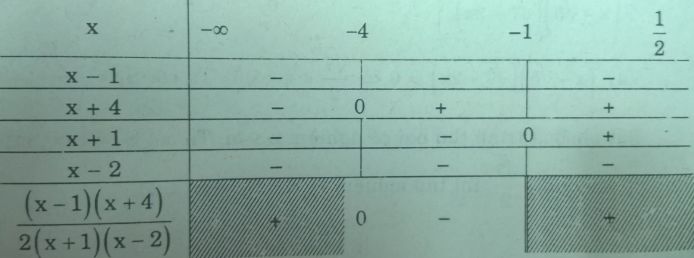
Suy ra tß║Łp nghiß╗ćm \(S_1 = \left( { - 4; - 1} \right)\)
Nß║┐u \(x > \frac{1}{2}\) thi bß║źt phŲ░ŲĪng tr├¼nh trß╗¤ th├Ānh:
\(\begin{array}{l}
\frac{{2x - 1}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} > \frac{1}{2}\\
\Leftrightarrow \frac{{2\left( {2x - 1} \right) - \left( {x + 1} \right)\left( {x - 2} \right)}}{{2\left( {x + 1} \right)\left( {x - 2} \right)}} > 0\\
\Leftrightarrow \frac{{x\left( {x - 5} \right)}}{{2\left( {x + 1} \right)\left( {x - 2} \right)}} < 0
\end{array}\)
Bß║Żng x├®t dß║źu
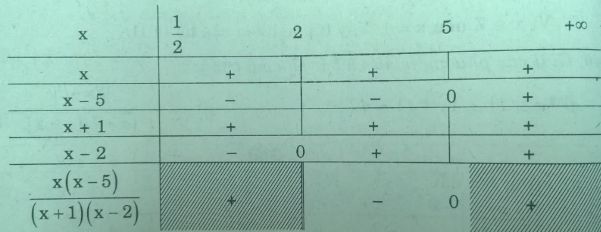
Suy ra tß║Łp nghiß╗ćm \(S_2=(2;5)\)
Vß║Ły tß║Łp nghiß╗ćm cß╗¦a bß║źt phŲ░ŲĪng tr├¼nh ─æ├Ż cho l├Ā \(S = {S_1} \cup {S_2} = \left( { - 4; - 1} \right) \cup \left( {2;5} \right)\)
B├Āi 41 trang 127 SGK To├Īn 10 n├óng cao
Giß║Żi v├Ā biß╗ćn luß║Łn bß║źt phŲ░ŲĪng tr├¼nh
a) \(\left\{ \begin{array}{l}
\left( {x - \sqrt 5 } \right)\left( {\sqrt 7 - 2x} \right) > 0\,\,\,(1)\\
x - m \le 0\,\,\,(2)
\end{array} \right.\)
b) \(\left\{ \begin{array}{l}
\frac{2}{{x - 1}} < \frac{5}{{2x - 1}}\,\,\,(1)\\
x - m \ge 0\,\,\,(2)
\end{array} \right.\)
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Giß║Żi (1):
Bß║Żng x├®t dß║źu
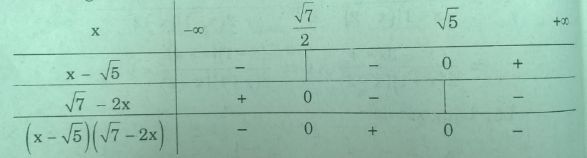
Suy ra \({S_1} = \left( {\frac{{\sqrt 7 }}{2};\sqrt 5 } \right)\)
Ta c├│ \(\left( 2 \right) \Leftrightarrow x \le m\), suy ra \({S_2} = \left( { - \infty ;m} \right]\)
Do đó:
Nß║┐u \(m \le \frac{{\sqrt 7 }}{2}\) th├¼ tß║Łp nghiß╗ćm l├Ā \(S = {S_1} \cap {S_2} = \emptyset \)
Nß║┐u \(\frac{{\sqrt 7 }}{2} \le m < \sqrt 5 \) th├¼ tß║Łp nghiß╗ćm l├Ā \(S = {S_1} \cap {S_2} = \left( {\frac{{\sqrt 7 }}{2};m} \right)\)
Nß║┐u \(m \ge \sqrt 5 \) thfi tß║Łp nghiß╗ćm l├Ā \(S = {S_1} \cap {S_2} = \left( {\frac{{\sqrt 7 }}{5};\sqrt 5 } \right)\)
Câu b:
\(\begin{array}{l}
\frac{2}{{x - 1}} < \frac{5}{{2x - 1}} \Leftrightarrow \frac{{2\left( {2x - 1} \right) - 5\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} < 0\\
\Leftrightarrow \frac{{x - 3}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} > 0
\end{array}\)
Bß║▒ng c├Īch lß║Łp bß║Żng x├®t dß║źu, ta c├│ tß║Łp nghiß╗ćm cß╗¦a (1) l├Ā \({S_1} = \left( {\frac{1}{2};1} \right) \cup \left( {3; + \infty } \right)\)
Ta lß║Īi c├│ \(\left( 2 \right) \Leftrightarrow x \ge m\), suy ra (2) c├│ tß║Łp nghiß╗ćm l├Ā \({S_2}=\left[ {m; + \infty } \right)\)
Do đó:
Nß║┐u \(x \le \frac{1}{2}\) th├¼ tß║Łp nghiß╗ćm l├Ā \(S = {S_1} \cap {S_2} = \left( {\frac{1}{2};1} \right) \cup \left( {3; + \infty } \right)\)
Nß║┐u \(\frac{1}{2} < m < 1\) th├¼ tß║Łp nghiß╗ćm l├Ā \(S = {S_1} \cap {S_2} = \left[ {m;1} \right) \cup \left( {3; + \infty } \right)\)
Nß║┐u \(1 \le m \le 3\) th├¼ tß║Łp nghiß╗ćm l├Ā \(S = \left( {3; + \infty } \right)\)
Nß║┐u m > 3 th├¼ tß║Łp nghiß╗ćm l├Ā \(S = \left[ {m; + \infty } \right)\)
Tr├¬n ─æ├óy l├Ā nß╗Öi dung chi tiß║┐t Giß║Żi b├Āi tß║Łp n├óng cao To├Īn 10 ChŲ░ŲĪng 4 Luyß╗ćn tß║Łp (trang 127) vß╗øi hŲ░ß╗øng dß║½n giß║Żi chi tiß║┐t, r├Ą r├Āng, tr├¼nh b├Āy khoa hß╗Źc. Hoc247 hy vß╗Źng ─æ├óy sß║Į l├Ā t├Āi liß╗ću hß╗»u ├Łch gi├║p c├Īc bß║Īn hß╗Źc sinh lß╗øp 10 hß╗Źc tß║Łp thß║Łt tß╗æt.
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm





.PNG)
.PNG)


