Giải Toán 10 SGK nâng cao Chương 4 Bài 6 Dấu của tam thức bậc hai

Xét dấu các tam thức bậc hai sau:

a) 3x² - 2x + 1

b) - x² + 4x – 1

c) \({x^2} - \sqrt 3 x + \frac{3}{4}\)

d) \(\left( {1 - \sqrt 2 } \right){x^2} - 2x + 1 + \sqrt 2 \)

Hướng dẫn giải:

Câu a:

Ta có:

a = 3 > 0

Δ’ = 1 – 3 = - 2 < 0

⇒ 3x² – 2x + 1 > 0, ∀x  ∈ R

Câu b:

Đặt f(x) = - x2 + 4x – 1

Ta có:

a = -1 < 0

Δ’ = 4 – 1 = 3 > 0

Tam thức - x² + 4x – 1 có hai nghiệm phân biệt \(x = 2 \pm \sqrt 3 \)

Bảng xét dấu

                     

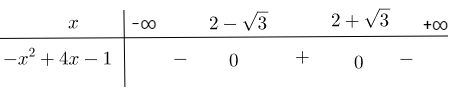
Vậy f(x) > 0 với mọi \(x \in \left( {2 - \sqrt 3 ;2 + \sqrt 3 } \right)\)

f(x) < 0 với mọi \(x \in \left( { - \infty ;2 - \sqrt 3 } \right) \cup \left( {2 + \sqrt 3 ; + \infty } \right)\)

Câu c:

Ta có:

a = 1 > 0

Δ = 3 – 3 = 0

 \({x^2} - \sqrt 3 x + \frac{3}{4}\) có nghiệm kép là \(x = \frac{{\sqrt 3 }}{2}\)

Suy ra \({x^2} - \sqrt 3 x + \frac{3}{4} > 0,\forall x \ne \frac{{\sqrt 3 }}{2}\)

Câu d:

Đặt f(x) = \(\left( {1 - \sqrt 2 } \right){x^2} - 2x + 1 + \sqrt 2 \)

\(\begin{array}{l}
a = 1 - \sqrt 2  < 0\\
\left( {1 - \sqrt 2 } \right){x^2} - 2x + 1 + \sqrt 2  = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x =  - 3 - 2\sqrt 2 
\end{array} \right.
\end{array}\)

Bảng xét dấu

Vậy f(x) > 0 với mọi \(x \in \left( { - 3 - 2\sqrt 3 ;1} \right)\)

f(x) < 0 với mọi \(\left( { - \infty ; - 3 - 2\sqrt 3 } \right) \cup \left( {1; + \infty } \right)\)

---

Tìm các giá trị của m để mỗi biểu thức sau luôn dương:

a) (m²+2)x² - 2(m+1)x + 1

b) (m+2)x² + 2(m+2)x + m + 3

Hướng dẫn giải:

Câu a:

Vì m² + 2 > 0 nên (m²+2)x² - 2(m+1)x + 1 > 0, ∀x ∈ R

⇔ Δ’ = (m + 1)² – (m² + 2) < 0 ⇔ 2m – 1 < 0

⇔ \(m < \frac{1}{2}\)

Vậy với \(m < \frac{1}{2}\) thì (m²+2)x² - 2(m+1)x + 1 > 0, ∀ x ∈ R

Câu b:

• Với m = - 2 thì \(f\left( x \right) = 1 > 0,\forall x \in R\)
• Với \(m \ne  - 2\) ta có \(f\left( x \right) > 0,\forall x \in R\)

\(\begin{array}{l}
 \Leftrightarrow \left\{ \begin{array}{l}
a > 0\\
\Delta ' < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m + 2 > 0\\
{\left( {m + 2} \right)^2} - \left( {m + 2} \right)\left( {m + 3} \right) < 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m >  - 2\\
 - m - 2 < 0
\end{array} \right. \Leftrightarrow m >  - 2
\end{array}\)

Vậy \(f\left( x \right) > 0,\forall x \in R \Leftrightarrow m \ge  - 2\)

---

Tìm các giá trị của m để mỗi biểu thức sau luôn âm.

a) \( - {x^2} + 2m\sqrt 2 x - 2{m^2} - 1\)

b) \(\left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1\)

Hướng dẫn giải:

Câu a:

Vì a = - 1 < 0 nên:

\(\begin{array}{l}
 - {x^2} + 2m\sqrt 2 x - 2{m^2} - 1 < 0,\forall x \in R\\
 \Leftrightarrow \Delta ' = 2{m^2} - \left( {2{m^2} + 1} \right) < 0\\
 \Leftrightarrow  - 1 < 0\,\,\left( {ld} \right)
\end{array}\)

Vậy với mọi m thì \( - {x^2} + 2m\sqrt 2 x - 2{m^2} - 1 < 0,\forall x \in R\)

Câu b:

Đặt \(f\left( x \right) = \left( {m - 2} \right){x^2} - 2\left( {m - 3} \right)x + m - 1\)

Với m = 2 thì \(f(x) = 2x + 1\) không thỏa mãn điều kiện yêu cầu bài toán.

Với \(m \ne 2\) thì \(f\left( x \right) < 0,\forall x \in R\)

\(\begin{array}{l}
 \Leftrightarrow \left\{ \begin{array}{l}
a < 0\\
\Delta ' < 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m - 2 < 0\\
{\left( {m - 3} \right)^2} - \left( {m - 2} \right)\left( {m - 1} \right) < 0
\end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m < 2\\
 - 3m + 7 < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m < 2\\
m > \frac{7}{3}
\end{array} \right.
\end{array}\)

Ta không tìm được m thỏa mãn hệ thức trên.

Vậy không có giá trị m để \(f\left( x \right) < 0,\forall x \in R\)

---

Chứng minh định lý về dấu của tam thức bậc 2.

Hướng dẫn: Với các trường hợp Δ < 0 và Δ = 0, sử dụng hệ thức đã biết:

\(f\left( x \right) = a\left[ {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right]\)

Hay \(af\left( x \right) = {a^2}\left[ {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right]\)

Trong trường hợp Δ > 0, sử dụng hệ thức đã biết:

f(x) = a(x – x₁)(x – x₂) hay af(x) = a²(x – x₁)(x – x₂)

trong đó x₁ và x₂ là hai nghiệm của tam thức bậc hai f(x)

Hướng dẫn giải:

Ta có: \(af\left( x \right) = {a^2}\left[ {{{\left( {x + \frac{b}{{2a}}} \right)}^2} - \frac{\Delta }{{4{a^2}}}} \right]\)

• Nếu Δ < 0 thì af(x) > 0 với mọi x ∈ R, tức f(x) cùng dấu với a với mọi x ∈ R
• Nếu Δ = 0 thì \(af\left( x \right) = {a^2}{\left( {x + \frac{b}{{2a}}} \right)^2}\) khi đó af(x) > 0 với mọi \(x \ne  - \frac{b}{{2a}}\)
• Nếu Δ > 0 thì f(x) có hai nghiệm phân biệt x₁ và x₂ và f(x) = a(x – x₁)(x – x₂)

Do đó: af(x) = a²(x – x₁)(x – x₂)

Vậy af(x) có cùng dấu với tích (x – x₁)(x – x₂).

Dấu của tích này được cho trong bảng sau (x₁ < x₂)

 

Do đó: af(x) < 0 với mọi x ∈ (x₁, x₂)

Và af(x) > 0 với mọi x < x₁ hoặc x > x₂