Mời các em học sinh lớp 10 cùng tham khảo tài liệu Hướng dẫn giải chi tiết bài tập SGK Toán 10 nâng cao Chương 4 Bài 5 Bất phương trình và hệ bất phương trình bậc nhất hai ẩn do HỌC247 tổng hợp và biên soạn dưới đây. Nội dung tài liệu bao gồm phương pháp giải và đáp án gợi ý được trình bày một cách khoa học và dễ hiểu, giúp các em dễ dàng vận dụng, nâng cao kỹ năng làm bài. Chúc các em học tốt!
Bài 42 trang 132 SGK Toán 10 nâng cao
Xác định miền nghiệm của mỗi bất phương trình hai ẩn
a)
b)
Hướng dẫn giải:
Câu a:
Ta có
Miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ là đường thẳng − x + 2y – 8 = 0 và không chứa gốc tọa độ O.
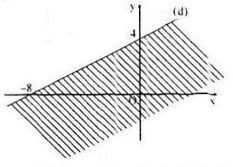
Câu b:
Miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ là đường thẳng và chứa gốc tọa độ O.
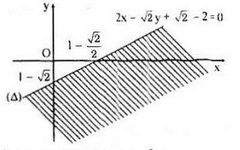
Bài 43 trang 132 SGK Toán 10 nâng cao
Xác định tập nghiệm của mỗi hệ bất phương trình hai ẩn
a)
b)
Hướng dẫn giải:
Câu a:
Ta có
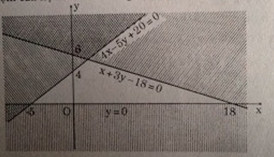
Miền nghiệm của hệ là miền không bị gạch chéo (không kể biên) như hình vẽ:

Câu b:
Ta có
Miền nghiệm của hệ là miền không bị gạch (không kể biên) trên hình.
Bài 44 trang 132 SGK Toán 10 nâng cao
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn (heo) chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng khi gia đình này chỉ mua nhiều nhất là 1,6 kg thịt bò, 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 45000đ, 1kg thịt lợn lầ 35000đ. Giả sử gia đình mua x kg thịt bò và y kg thịt lợn.
a) Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm (S) của hệ đó.
b) Gọi T (nghìn đồng) là số tiền phải trả cho x (kilogam) thịt bò và y (kilogam) thịt lợn. Hãy biểu diễn T theo x, y
c) Ở câu a) ta thấy (S) là một miền đa giác. Biết rằng T có giá trị nhỏ nhất tại (x0;y0) với (x0;y0) là tọa độ của một trong các đỉnh của (S). Hỏi gia đình đó phải mua bao nhiêu kilogam thịt mỗi loại để chi phí ít nhất.
Hướng dẫn giải:
Câu a:
Giả sử gia đình đó mua x (kg) thịt bò và y (kg) thịt lợn,
Theo giả thiết, x và y cần thỏa mãn điều kiện: 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1
Khi đó, số đơn vị protein có được là 800x + 600y và số đơn vị lipit có được là 200x + 400y.
Vì gia đình đó cần ít nhất 400 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là:
800x + 600y ≥ 900 và 200x + 400y ≥ 400
Hay 4x + 3y ≥ 4,5 và x + 2y ≥ 2
Vậy các điều kiện mà x và y thỏa mãn là:
Miền nghiệm của hệ trên miền tứ giác ABCD (kể cả biên) trên hình.
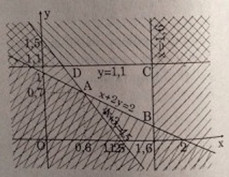
Câu b:
Chi phí để mua x (kg) thịt bò và y (kg) thịt kợn là:
T = 45x + 35y (nghìn đồng)
Câu c:
Ta cần tìm (x, y) sao cho T nhỏ nhất
Ta biết T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.
Tại A(0,6;0,7) ta có T = 45.0,6 + 35.0,7 = 51,5 (nghìn đồng)
Tại B(1,6;0,2) ta có T = 45.1,6 + 35.02 = 79 (nghìn đồng)
Tại C(1,6;1,1) ta có T = 4,5.1,6 + 35.1,1 = 110,5 (nghìn đồng)
Tại D(0,3;1,1) ta có T = 45.0,3 + 35.11 = 52 (nghìn đồng)
Vậy khi x = 0,6 và y = 0,7 thì T đạt giá trị nhỏ nhất
Trả lời: gia đình đó mua 0,6kg thịt bò và 0,7kg thịt lợn thì chi phí ít nhất.
Cụ thể, chi phí là 51,5 nghìn đồng.
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 4 Bài 5 Bất phương trình và hệ bất phương trình bậc nhất hai ẩn với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
Tư liệu nổi bật tuần
- Xem thêm







