Dưới đây là Hướng dẫn giải bài tập Toán 10 nâng cao Chương 4 Bài 4 Dấu của nhị thức bậc nhất được hoc247 biên soạn và tổng hợp, nội dung bám sát theo chương trình SGK Đại số 10 nâng cao giúp các em học sinh nắm vững phương pháp giải bài tập và ôn tập kiến thức hiệu quả hơn.
Bài 32 trang 126 SGK Toán 10 nâng cao
Lập bảng xét dấu của các biểu thức
a) \(\frac{{4 - 3x}}{{2x + 1}}\)
b) \(1 - \frac{{2 - x}}{{3x - 2}}\)
c) \(x{\left( {x - 2} \right)^2}\left( {3 - x} \right)\)
d) \(\frac{{x{{\left( {x - 3} \right)}^2}}}{{\left( {x - 5} \right)\left( {1 - x} \right)}}\)
Hướng dẫn giải:
Câu a:
Đặt \(f(x)=\frac{{4 - 3x}}{{2x + 1}}\)
Ta có:
\(\begin{array}{l}
4 - 3x = 0 \Leftrightarrow x = \frac{4}{3}\\
2x + 1 = 0 \Leftrightarrow x = - \frac{1}{2}
\end{array}\)
Bảng xét dấu
.jpg?enablejsapi=1)
Vậy \(f\left( x \right) < 0\) với \(x \in \left( { - \infty ; - \frac{1}{2}} \right) \cup \left( {\frac{4}{3}; + \infty } \right)\)
\(f\left( x \right) > 0\) với \(x \in \left( { - \frac{1}{2};\frac{4}{3}} \right)\)
\(f(x)=0\) tại \(x = \frac{4}{3}\)
Câu b:
Đặt \(f(x) = 1 - \frac{{2 - x}}{{3x - 2}} = \frac{{3x - 2 - 2 + x}}{{3x - 2}} = \frac{{4x - 4}}{{3x - 2}}\)
Ta có:
\(\begin{array}{l}
4x - 4 = 0 \Leftrightarrow x = 1\\
3x - 2 = 0 \Leftrightarrow x = \frac{2}{3}
\end{array}\)
Bảng xét dấu
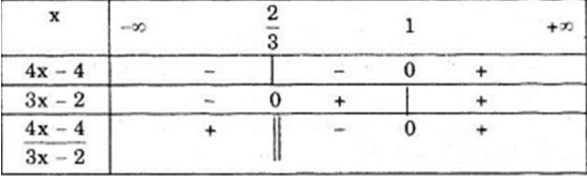
Vậy \(f\left( x \right) < 0\) với \(\left( {\frac{2}{3};1} \right)\)
\(f\left( x \right) > 0\) với \(\left( { - \infty ;\frac{2}{3}} \right) \cup \left( {1; + \infty } \right)\)
\(f(x)=0\) tại x = 1
Câu c:
Đặt \(f(x)=x{\left( {x - 2} \right)^2}\left( {3 - x} \right)\)
Ta có:
\(\begin{array}{l}
x = 0\\
x - 2 = 0 \Leftrightarrow x = 2\\
3 - x = 0 \Leftrightarrow x = 3
\end{array}\)
Bảng xét dấu
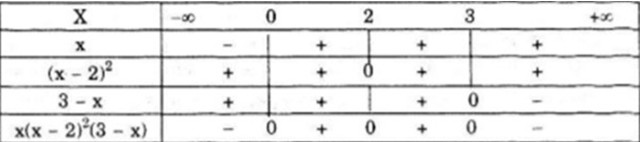
Vậy \(f\left( x \right) < 0\) với \(\left( { - \infty ;0} \right) \cup \left( {3; + \infty } \right)\)
\(f\left( x \right) > 0\) với \(\left( {0;2} \right) \cup \left( {2;3} \right)\)
\(f(x)=0\) tại x = 0, x = 2 và x = 3
Câu d:
Đặt \(f(x)=\frac{{x{{\left( {x - 3} \right)}^2}}}{{\left( {x - 5} \right)\left( {1 - x} \right)}}\)
Ta có:
\(\begin{array}{l}
x = 0\\
x - 3 = 0 \Leftrightarrow x = 3\\
x - 5 = 0 \Leftrightarrow x = 5\\
1 - x = 0 \Leftrightarrow x = 1
\end{array}\)
Bảng xét dấu
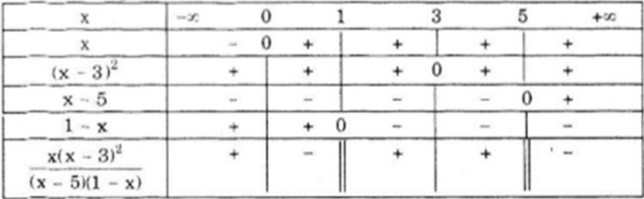
Vậy \(f\left( x \right) < 0\) với \(\left( {0;1} \right) \cup \left( {5; + \infty } \right)\)
\(f\left( x \right) > 0\) với \(\left( { - \infty ;0} \right) \cup \left( {1;3} \right) \cup \left( {3;5} \right)\)
\(f(x)=0\) tại x = 0 và x = 3
Bài 33 trang 126 SGK Toán 10 nâng cao
Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:
a) \(-x^2+x+6\)
b) \(2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \)
Hướng dẫn giải:
Câu a:
Đặt \(f(x)=-x^2+x+6\)
Ta có \( f(x)=- {x^2} + x + 6 = - \left( {x + 2} \right)\left( {x - 3} \right) = \left( { - x - 2} \right)\left( {x - 3} \right)\)
Bảng xét dấu
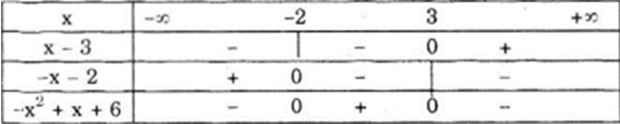
Vậy \(f\left( x \right) < 0\) với \(\left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right)\)
\(f\left( x \right) > 0\) với (- 2;3)
\(f(x)=0\) tại x = - 2 và x = 3
Câu b:
Đặt \(f(x)=2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \)
Ta có \(f(x) = 2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 = 2\left( {x - 1} \right)\left( {x - \frac{{\sqrt 3 }}{2}} \right) = \left( {x - 1} \right)\left( {2x - \sqrt 3 } \right)\)
Bảng xét dấu
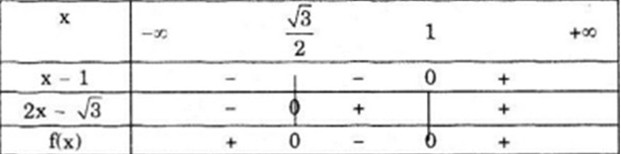
Vậy \(f\left( x \right) < 0\) với \({\left( {\frac{{\sqrt 3 }}{2};1} \right)}\)
\(f\left( x \right) > 0\) với \(\left( { - \infty ;\frac{{\sqrt 3 }}{2}} \right) \cup \left( {1; + \infty } \right)\)
\(f(x)=0\) tại \(x={\frac{{\sqrt 3 }}{2}}\) và x = 1
Bài 34 trang 126 SGK Toán 10 nâng cao
Giải các bất phương trình
a) \(\frac{{\left( {3 - x} \right)\left( {x - 2} \right)}}{{x + 1}} \le 0\)
b) \(\frac{3}{{1 - x}} \ge \frac{5}{{2x + 1}}\)
c) \(\left| {2x - \sqrt 2 } \right| + \left| {\sqrt 2 - x} \right| > 3x - 2\)
d) \(\left| {\left( {\sqrt 2 - \sqrt 3 } \right)x + 1} \right| \le \sqrt 3 + \sqrt 2 \)
Hướng dẫn giải:
Câu a:
Ta có:
\(\begin{array}{l}
3 - x = 0 \Leftrightarrow x = 3\\
x - 2 = 0 \Leftrightarrow x = 2\\
x + 1 = 0 \Leftrightarrow x = - 1
\end{array}\)
Bảng xét dấu
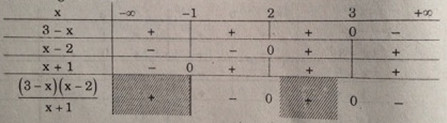
Vậy tập nghiệm là \(S = \left( { - 1;2} \right] \cup \left[ {3; + \infty } \right)\)
Câu b:
Ta có \(\frac{3}{{1 - x}} \ge \frac{5}{{2x + 1}} \Leftrightarrow \frac{{3\left( {2x + 1} \right) - 5\left( {1 - x} \right)}}{{\left( {1 - x} \right)\left( {2x + 1} \right)}} \ge 0 \Leftrightarrow \frac{{11x - 2}}{{\left( {1 - x} \right)\left( {2x + 1} \right)}} \ge 0\)
\(\begin{array}{l}
11x - 2 = 0 \Leftrightarrow x = \frac{2}{{11}}\\
1 - x = 0 \Leftrightarrow x = 1\\
2x + 1 = 0 \Leftrightarrow x = - \frac{1}{2}
\end{array}\)
Bảng xét dấu
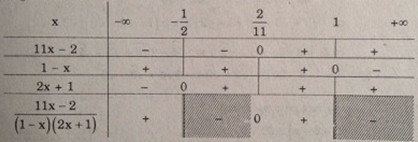
Vậy tập nghiệm của bất phương trình đã cho là \(S = \left( { - \infty ; - \frac{1}{2}} \right) \cup \left[ {\frac{2}{{11}};1} \right)\)
Câu c:
Bảng xét dấu

Với \(x < \frac{{\sqrt 2 }}{2}\), ta có:
\(\begin{array}{l}
pt \Leftrightarrow - 2x + \sqrt 2 + \sqrt 2 - x > 3x - 2\\
\Leftrightarrow 6x < 2\sqrt 2 + 2\\
\Leftrightarrow x < \frac{{\sqrt 2 + 1}}{3}
\end{array}\)
Kết hợp với điều kiện ta có \(x < \frac{{\sqrt 2 }}{2}\)
Với \(\frac{{\sqrt 2 }}{2} \le x < \sqrt 2 \), ta có:
\(pt \Leftrightarrow 2x - \sqrt 2 + \sqrt 2 - x > 3x - 2 \Leftrightarrow x < 1\)
Kết hợp với điều kiện ta có \(\frac{{\sqrt 2 }}{2} \le x < 1\)
Với \(x \ge \sqrt 2 \), ta có:
\(pt \Leftrightarrow 2x - \sqrt 2 - \sqrt 2 + x > 3x - 2 \Leftrightarrow 0x > - 2 + 2\sqrt 2 \) (vô nghiệm)
Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ;\frac{{\sqrt 2 }}{2}} \right) \cup \left[ {\frac{{\sqrt 2 }}{2};1} \right) = \left( { - \infty ;1} \right)\)
Câu d:
\(\begin{array}{l}
\left| {\left( {\sqrt 2 - \sqrt 3 } \right)x + 1} \right| \le \sqrt 3 + \sqrt 2 \\
\Leftrightarrow - \sqrt 3 - \sqrt 2 \le \left( {\sqrt 2 - \sqrt 3 } \right)x + 1 \le \sqrt 3 + \sqrt 2 \\
\Leftrightarrow - \sqrt 3 - \sqrt 2 - 1 \le \left( {\sqrt 2 - \sqrt 3 } \right)x \le \sqrt 3 + \sqrt 2 - 1\\
\Leftrightarrow \frac{{ - \sqrt 3 - \sqrt 2 - 1}}{{\sqrt 2 - \sqrt 3 }} \ge x \ge \frac{{\sqrt 3 + \sqrt 2 - 1}}{{\sqrt 2 - \sqrt 3 }}\\
\Leftrightarrow \left( {\sqrt 3 + \sqrt 2 + 1} \right)\left( {\sqrt 3 + \sqrt 2 } \right) \ge x \ge \left( {1 - \sqrt 3 - \sqrt 2 } \right)\left( {\sqrt 3 + \sqrt 2 } \right)\\
\Leftrightarrow 5 + 2\sqrt 6 + \sqrt 3 + \sqrt 2 \ge x \ge - 5 - 2\sqrt 6 + \sqrt 3 + \sqrt 2
\end{array}\)
Vậy \(S = \left[ { - 5 - 2\sqrt 6 + \sqrt 3 + \sqrt 2 ;5 + 2\sqrt 6 + \sqrt 3 + \sqrt 2 } \right]\)
Bài 35 trang 126 SGK Toán 10 nâng cao
Giải các hệ phương trình
a) \(\left\{ \begin{array}{l}
\left( {x - 3} \right)\left( {\sqrt 2 - x} \right) > 0\\
\frac{{4x - 3}}{2} < x + 3
\end{array} \right.\)
b) \(\left\{ \begin{array}{l}
\frac{2}{{2x - 1}} \le \frac{1}{{3 - x}}\\
\left| x \right| < 1
\end{array} \right.\)
Hướng dẫn giải:
Câu a:
\(\left\{ {\begin{array}{*{20}{l}}
{\left( {x - 3} \right)\left( {\sqrt 2 - x} \right) > 0\,\,\,\left( 1 \right)}\\
{\frac{{4x - 3}}{2} < x + 3\,\,\,\left( 2 \right)}
\end{array}} \right.\)
Giải (1):
Bảng xét dấu
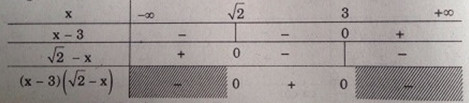
Suy ra tập nghiệm \({S_1} = \left( {\sqrt 2 ;3} \right)\)
Giải (2):
\(\left( 2 \right) \Leftrightarrow 4x - 3 < 2x + 6 \Leftrightarrow 2x < 9 \Leftrightarrow x < \frac{9}{2}\)
Vậy \(S = {S_1} \cap {S_2} = \left( {\sqrt 2 ;3} \right)\)
Câu b:
\(\left\{ {\begin{array}{*{20}{l}}
{\frac{2}{{2x - 1}} \le \frac{1}{{3 - x}}\,\,\,\left( 1 \right)}\\
{ - 1 < x < 1}
\end{array}} \right.\)
Giải (1):
\(\begin{array}{l}
\frac{2}{{2x - 1}} \le \frac{1}{{3 - x}} \Leftrightarrow \frac{2}{{2x - 1}} - \frac{1}{{3 - x}} \le 0\\
\Leftrightarrow \frac{{6 - 2x - 2x + 1}}{{\left( {2x - 1} \right)\left( {3 - x} \right)}} \le 0 \Leftrightarrow \frac{{ - 4x + 7}}{{\left( {2x + 1} \right)\left( {3 - x} \right)}} \le 0
\end{array}\)
Bảng xét dấu
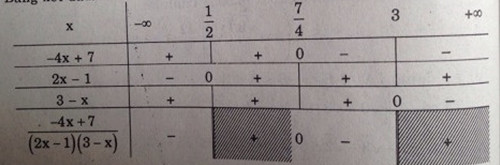
Suy ra tập nghiệm \({S_1} = \left( { - \infty ;\frac{1}{2}} \right) \cup \left[ {\frac{7}{4};3} \right)\)
Kết hợp với - 1 < x < 1 ta có tập nghiệm của hệ là \(S = \left( { - 1;\frac{1}{2}} \right)\)
Tư liệu nổi bật tuần
- Xem thêm







