Giải Toán 10 SGK nâng cao Chương 3 Bài 2 Phương trình bậc nhất và phương trình bậc hai một ẩn

Xem các bài giải sau đây và cho biết mỗi bài giải đó đúng hay sai? Vì sao?

a) \(\frac{{\left( {x - 2} \right)\left( {x - 1} \right)}}{{\sqrt x  - 1}} = 0\)

\(\begin{array}{l}
 \Leftrightarrow \frac{{x - 2}}{{\sqrt x  - 1}}\left( {x - 1} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\frac{{x - 2}}{{\sqrt x  - 1}} = 0\\
x - 1 = 0
\end{array} \right.
\end{array}\)

Ta có \(\frac{{x - 2}}{{\sqrt x  - 1}} = 0 \Leftrightarrow x = 2\)

\(x - 1 = 0 \Leftrightarrow x = 1\)

Vậy tập nghiệm của phương trình đã cho là S = {1, 2}

b) \(\sqrt {{x^2} - 2}  = 1 - x \Leftrightarrow {x^2} - 2 = {\left( {1 - x} \right)^2}\)

\( \Leftrightarrow {x^2} - 2 = 1 - 2x + {x^2} \Leftrightarrow 2x = 3 \Leftrightarrow x = \frac{3}{2}\)

Vậy phương trình có nghiệm \(x = \frac{3}{2}\)

Hướng dẫn giải:

Câu a:

Sai khi kết luận tập nghiệm: x = 1 không thuộc ĐKXĐ của phương trình

Câu b:

Sai vì khi bình thường hai vế chỉ được phương trình hệ quả. Nhất thiết phải thử lại giá trị x tìm được.

---

Giải và biện luận các phương trình

a) \((m^2+2)x-2m=x-3\)

b) \(m(x-m)=x+m-2\)

c) \(m(x-m+3)=m(x-2)+6\)

d) \(m^2(x-1)+m=x(3m-2)\)

Hướng dẫn giải:

Câu a:

Ta có \(({m^2} + 2)x - 2m = x - 3 \Leftrightarrow \left( {{m^2} + 1} \right)x = 2m - 3\)

Vì \({{m^2} + 1 \ne 0,\forall m}\) nên phương trình có nghiệm duy nhất \(x = \frac{{2m + 3}}{{{m^2} + 1}}\)

Câu b:

\(\begin{array}{l}
m\left( {x - m} \right) = x + m - 2 \Leftrightarrow mx - x = {m^2} + m - 2\\
 \Leftrightarrow \left( {m - 1} \right)x = \left( {m - 1} \right)\left( {m + 2} \right)
\end{array}\)

• Nếu \(m \ne 1\) thì phương trình có nghiệm duy nhất \(x = \frac{{\left( {m - 1} \right)\left( {m + 2} \right)}}{{m - 1}} = m + 2\)
• Nếu m = 1 thì 0x = 0, phương trình có tập nghiệm S = R.

Câu c:

\(\begin{array}{l}
m\left( {x - m + 3} \right) = m\left( {x - 2} \right) + 6\\
 \Leftrightarrow mx - {m^2} + 3m = mx - 2m + 6\\
 \Leftrightarrow 0x = {m^2} - 5m + 6\\
 \Leftrightarrow 0x = \left( {m - 2} \right)\left( {m - 3} \right)
\end{array}\)

• Nếu m = 2 hoặc m = 3 thì phương trình có tập nghiệm S = R
• Nếu \(m \ne 2\) và \(m \ne 3\) thì phương trình vô nghiệm.

---

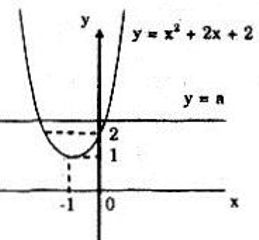
Dựa vào hình bên, tìm các giá trị của a để phương trình: \(3x+2=−x^2+x+a\) có nghiệm dương.

Khi đó, hãy tìm nghiệm dương của phương trình.

 

Hướng dẫn giải:

Ta có \(3x + 2 =  - {x^2} + x + a \Leftrightarrow {x^2} + 2x + 2 = a\)

Nghiệm của phương trình là hoành độ giao điểm của (P): \(x^2+2x+2\) và đường thẳng d: \(y = a\)

Dựa vào đồ thị ta có:

Phương trình có nghiệm dương khi và chỉ khi \(a > 2\), khi đó nghiệm dương của phương trình là \(x =  - 1 + \sqrt {a - 1} \)

---

Giải và biện luận các phương trình

a) \((m-1)x^2+3x-1=0\)

b) \(x^2-4x+m-3=0\)

Hướng dẫn giải:

Câu a:

\((m-1)x^2+3x-1=0\)

• Với m = 1, phương trình trở thành \(3x - 1 = 0 \Leftrightarrow x = \frac{1}{3}\)
• Với \(m \ne 1\), ta có \(\Delta  = 9 + 4\left( {m - 1} \right) = 4m + 5\)

\(\Delta  < 0 \Leftrightarrow m <  - \frac{5}{4}\): Phương trình vô nghiệm

\(\Delta  = 0 \Leftrightarrow m =  - \frac{5}{4}\): Phương trình có nghiệm kép \({x_1} = {x_2} =  - \frac{b}{{2a}} = \frac{{ - 3}}{{2\left( {m - 1} \right)}} = \frac{{ - 3}}{{2\left( { - \frac{5}{4} - 1} \right)}} = \frac{2}{3}\)

\(\Delta  > 0 \Leftrightarrow m >  - \frac{5}{4}\): Phương trình có hai nghiệm phân biệt \({x_{1,2}} = \frac{{ - 3 \pm \sqrt {4m + 5} }}{{2\left( {m - 1} \right)}}\)

Câu b:

\(x^2-4x+m-3=0\)

Ta có: \(\Delta ' = 4 - \left( {m - 3} \right) = 7 - m\)

• \(\Delta ' < 0 \Leftrightarrow m > 7\): Phương trình vô nghiệm
• \(\Delta ' = 0 \Leftrightarrow m = 7\): Phương trình có nghiệm kép \({x_1} = {x_2} =  - \frac{b}{{2a}} = \frac{4}{2} = 2\)
• \(\Delta ' > 0 \Leftrightarrow m > 7\): Phương trình có hai nghiệm phân biệt \({x_{1,2}} = 2 \pm \sqrt {7 - m} \)

---

a) Giả sử phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁ và x₂.

Chứng minh rằng:  ax² + bx + c = a(x – x₁)(x – x₂)

b) Áp dụng: Phân tích các đa thức sau thành nhân tử

\(f(x)=-2x^2-7x+4\);

\(g\left( x \right) = \left( {\sqrt 2  + 1} \right){x^2} - 2\left( {\sqrt 2  + 1} \right)x + 2\)

Hướng dẫn giải:

Câu a:

Áp dụng định lý Vi-ét, ta có: \(\left\{ {\begin{array}{*{20}{l}}
{{x_1} + {x_2} =  - \frac{b}{a}}\\
{{x_1}.{x_2} = \frac{c}{a}}
\end{array}} \right.\)

Do đó 

\(\begin{array}{*{20}{l}}
{a{x^2} + bx + c = 0 = a\left( {{x^2} + \frac{b}{a}x + \frac{c}{a}} \right)}\\
{ = a\left[ {{x^2} - \left( {{x_1} + {x_2}} \right)x + {x_1}{x_2}} \right]}\\
{ = a\left[ {x\left( {x - {x_1}} \right) - {x_2}\left( {x - {x_1}} \right)} \right]}\\
{ = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)}
\end{array}\)

Câu b:

Ta có \(f\left( x \right) =  - 2{x^2} - 7x + 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x =  - 4}\\
{x = \frac{1}{2}}
\end{array}} \right.\)

Do đó: \(f\left( x \right) =  - 2\left( {x + 4} \right)\left( {x - \frac{1}{2}} \right) = \left( {x + 4} \right)\left( {1 - 2x} \right)\)

Ta có \(g\left( x \right) = \left( {\sqrt 2  + 1} \right){x^2} - 2\left( {\sqrt 2  + 1} \right)x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \sqrt 2 }\\
{x = \frac{{\sqrt 2 }}{{\sqrt 2  + 1}}}
\end{array}} \right.\)

Do đó: \(g\left( x \right) = \left( {\sqrt 2  + 1} \right)\left( {x - \sqrt 2 } \right)\left( {x - \frac{{\sqrt 2 }}{{\sqrt 2  + 1}}} \right) = \left( {x - \sqrt 2 } \right)\left[ {\left( {\sqrt 2  + 1} \right)x - \sqrt 2 } \right]\)

---

Không giải phương trình x² - 2x - 15 = 0, hãy tính:

a) Tổng các bình phương hai nghiệm của nó.

b) Tổng các lập phương hai nghiệm của nó.

c) Tổng các lũy thừa bậc bốn hai nghiệm của nó.

Hướng dẫn: \(x_1^4 + x_2^4 = {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2\)

Hướng dẫn giải:

Vì \(ac=-15 < 0\) nên phương trình có hai nghiệm trái dấu

Theo định lý Vi-ét, ta có:

\({\left\{ \begin{array}{l}
{x_1} + {x_2} =  - \frac{b}{a} = 2\\
{x_1}.{x_2} = \frac{c}{a} =  - 15
\end{array} \right.}\)

Câu a:

Ta có \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {2^2} - 2\left( { - 15} \right) = 34\)

Câu b:

Ta có \(x_1^3 + x_2^3 = \left( {{x_1} + {x_2}} \right)\left( {x_1^2 - {x_1}{x_2} + x_2^2} \right)\)

\(\begin{array}{l}
 = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right]\\
 = 2.\left[ {4 - 3\left( { - 15} \right)} \right] = 98
\end{array}\)

Câu c:

Ta có \(x_1^4 + x_2^4 = {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2 = {34^2} - 2{\left( { - 15} \right)^2} = 706\)

---

Trong các khẳng định sau đây có duy nhất khẳng định đúng. Hãy chọn khẳng định đó. Phương trình: \(\left( {\sqrt 3  - 1} \right){x^4} + {x^2} + 2\left( {1 - \sqrt 3 } \right) = 0\).

(A) Vô nghiệm;

(B) Có hai nghiệm \(x =  \pm \frac{1}{2}\sqrt {\left( {1 + \sqrt 3 } \right)\left( {\sqrt {33 - 16\sqrt 3 }  - 1} \right)} \);

(C) Có bốn nghiệm \(x =  \pm \frac{1}{2}\sqrt {\left( {1 + \sqrt 3 } \right)\left( {\sqrt {33 - 16\sqrt 3 }  - 1} \right)} \) và \(x =  \pm \sqrt 3 \)

(D) Có hai nghiệm \(x =  \pm \sqrt 3 \)

Hướng dẫn giải:

Thay \(x = \sqrt 3 \) vào phương trình ta có ngay \(x = \sqrt 3 \) không là nghiệm, do vậy các khẳng định (C) và (D) là sai. Khẳng định (A) cũng sai vì phương trình đã cho có hệ số \(a = \sqrt 3  - 1 > 0,c = 2\left( {1 - \sqrt 3 } \right) < 0\) điều này chứng tỏ phương trình bậc hai \(\left( {\sqrt 3  - 1} \right){y^2} + y + 2\left( {1 - \sqrt 3 } \right) = 0\) có một nghiệm dương hay phương trình ban đầu phải có hai nghiệm phân biệt.

Vậy chỉ có khẳng định (B) là đúng (vì có duy nhất một khẳng định đúng).

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 3 Bài 2 Phương trình bậc nhất và phương trình bậc hai một ẩn với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.