Mời các em học sinh lớp 10 cùng tham khảo tài liệu Hướng dẫn giải chi tiết bài tập SGK Toán 10 nâng cao Chương 1 Bài 2 Tổng của hai vectơ do HỌC247 tổng hợp và biên soạn dưới đây. Nội dung tài liệu bao gồm phương pháp giải và đáp án gợi ý được trình bày một cách khoa học và dễ hiểu, giúp các em dễ dàng vận dụng, nâng cao kỹ năng làm bài. Chúc các em học tốt!
Bài 6 trang 14 SGK Hình học 10 nâng cao
Chứng minh rằng nếu \(\overrightarrow {AB} = \overrightarrow {CD} \) thì \(\overrightarrow {AC} = \overrightarrow {BD} \)
Hướng dẫn giải:
Áp dụng quy tắc 3 điểm, ta có:
\(\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BD} \Leftrightarrow \overrightarrow {AC} = \overrightarrow {BD} \)
Bài 7 trang 14 SGK Hình học 10 nâng cao
Tứ giác ABCDABCD là hình gì nếu \(\overrightarrow {AB} = \overrightarrow {DC} \) và \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)?
Hướng dẫn giải:
Từ \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left\{ \begin{array}{l}
AB//DC\\
AB = DC
\end{array} \right.\)
Suy ra ABCD là hình bình hành.
Mặt khác: AB, BC là hai cạnh liên tiếp của hình bình hành ABCD và AB = BC nên ABCD là hình thoi.
Bài 8 trang 14 SGK Hình học 10 nâng cao
Cho bốn điểm bất kì M, N, P, Q. Chứng minh các đẳng thức sau:
\(\begin{array}{l}
a)\overrightarrow {PQ} + \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MQ} \\
b)\overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {QP} + \overrightarrow {MQ} \\
c)\overrightarrow {MN} + \overrightarrow {PQ} = \overrightarrow {MQ} + \overrightarrow {PN}
\end{array}\)
Hướng dẫn giải:
Câu a:
Ta có \(\overrightarrow {PQ} + \overrightarrow {NP} + \overrightarrow {MN} = \left( {\overrightarrow {MN} + \overrightarrow {NP} } \right) + \overrightarrow {PQ} = \overrightarrow {MP} + \overrightarrow {PQ} = \overrightarrow {MQ} \) (đpcm)
Câu b:
\(\begin{array}{l}
\overrightarrow {NP} + \overrightarrow {MN} = \left( {\overrightarrow {NQ} + \overrightarrow {QP} } \right) + \left( {\overrightarrow {MQ} + \overrightarrow {QN} } \right)\\
= \overrightarrow {QP} + \overrightarrow {MQ} + \overrightarrow {NQ} + \overrightarrow {QN} = \overrightarrow {QP} + \overrightarrow {MQ}
\end{array}\)
Câu c:
\(\begin{array}{l}
\overrightarrow {MN} + \overrightarrow {PQ} = \left( {\overrightarrow {MQ} + \overrightarrow {QN} } \right) + \left( {\overrightarrow {PN} + \overrightarrow {NQ} } \right)\\
= \overrightarrow {MQ} + \overrightarrow {PN} + \overrightarrow {QN} + \overrightarrow {NQ} = \overrightarrow {MQ} + \overrightarrow {PN}
\end{array}\)
Bài 9 trang 14 SGK Hình học 10 nâng cao
Các hệ thức sau đây đúng hay sai (với mọi \(\overrightarrow a\) và \(\overrightarrow b\)) ?
a) \(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b }\right| \)
b) \(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Hướng dẫn giải:
Lấy \(\overrightarrow {AB} = \overrightarrow a \). từ B dựng \(\overrightarrow {BC} = \overrightarrow b \):
Khi đó \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow a + \overrightarrow b \). Xét 3 điểm A, B, C ta có:
\(AC \le AB + BC \Leftrightarrow \left| {\overrightarrow {AC} } \right| \le \left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {BC} } \right|\) hay \(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Dấu "=" xảy ra khi A, B, C thẳng hàng hay \(\overrightarrow a, \overrightarrow b\) cùng hướng. Do đó:
a) Sai
b) Đúng
Bài 10 trang 14 SGK Hình học 10 nâng cao
Cho hình bình hành ABCDABCD với tâm OO. Hãy điền vào chỗ trống (…) để được đẳng thức đúng
\(\begin{array}{l}
a)\overrightarrow {AB} + \overrightarrow {AD} = ...\\
b)\overrightarrow {AB} + \overrightarrow {CD} = ...\\
c)\overrightarrow {AB} + \overrightarrow {OA} = ...\\
d)\overrightarrow {OA} + \overrightarrow {OC} = ...\\
e)\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = ...
\end{array}\)
Hướng dẫn giải:
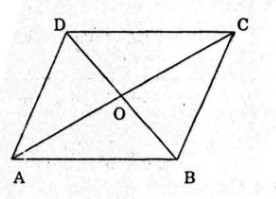
Câu a:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành)
Câu b:
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow 0 \)
Câu c:
\(\overrightarrow {AB} + \overrightarrow {OA} = \overrightarrow {AB} + \overrightarrow {OB} + \overrightarrow {BA} = \overrightarrow {OB} \) (quy tắc 3 điểm)
Câu d:
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) (vì O là trung điểm của AC)
Câu e:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \) (vì O là trung điểm của AC, BD)
Bài 11 trang 14 SGK Hình học 10 nâng cao
Cho hình bình hành ABCD với tâm O. Mỗi khẳng định sau đây đúng hay sai ?
\(\begin{array}{l}
a)\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BD} } \right|\\
b)\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {BC} \\
c)\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \\
d)\overrightarrow {BD} + \overrightarrow {AC} = \overrightarrow {AD} + \overrightarrow {BC}
\end{array}\)
Hướng dẫn giải:
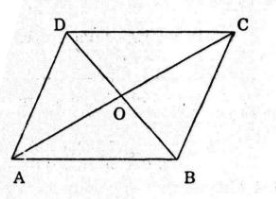
Câu a:
Sai vì \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| \ne \left| {\overrightarrow {BD} } \right|\)
Câu b:
Đúng vì \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \)
Câu c:
Sai. Vì
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = \left( {\overrightarrow {OC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {OD} + \overrightarrow {DB} } \right)\\
= \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {CA} + \overrightarrow {DB} } \right) \ne \overrightarrow {OC} + \overrightarrow {OD}
\end{array}\)
Câu d:
Đúng. Vì
\(\begin{array}{l}
\overrightarrow {BD} + \overrightarrow {AC} = \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right)\\
= \left( {\overrightarrow {DC} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {AD} } \right) = \overrightarrow {AD} + \overrightarrow {BC}
\end{array}\)
Bài 12 trang 14 SGK Hình học 10 nâng cao
Cho tam giác đều ABC nội tiếp đường tròn tâm O.
a) Hãy xác định các điểm M, N, P sao cho
\(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} ;\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} ;\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \)
b) Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \)
Hướng dẫn giải:
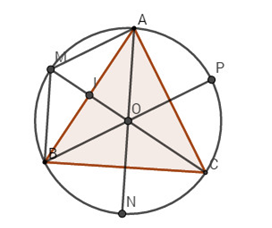
Câu a:
Theo quy tắc hình bình hành, ta có AOBM là hình bình hành.
Ta có AB, OM cắt nhau tại trung điểm mỗi đường, gọi I là trung điểm ABthì OI = IM. O là trọng tâm tam giác ABC nên OC = 2OI = OM.
Do đó O là trung điểm của MC, tức là MC là đường kính của đường tròn.
Vậy điểm M là điểm sao cho CM là đường kính của đường tròn tâm O.
Tương tự, ta cũng có N, P thuộc đường tròn (O) sao cho AN, BP là đường kính của đường tròn (O).
Câu b:
O là trung điểm của MC nên \(\overrightarrow {OM} + \overrightarrow {OC} = \overrightarrow 0 \) mà \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \)
Bài 13 trang 15 SGK Hình học 10 nâng cao
Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt tại O (h.17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau
a) \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều có cường độ là 100N, góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng 1200 (h.17a);
b) Cường độ của \(\overrightarrow {{F_1}} \) là 40N, của \(\overrightarrow {{F_2}} \) là 30N và góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng (h.17b).
.jpg)
Hướng dẫn giải:
Câu a:
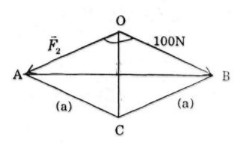
Ta lấy \(\overrightarrow {{F_2}} = \overrightarrow {OA} ,\overrightarrow {{F_1}} = \overrightarrow {OB} \).
Theo quy tắc hình bình hành, ta vẽ hình bình hành OACB.
Hình bình hành OACB có OA = OB nên OACB là hình thoi.
Ta có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \), OC là phân giác góc \(\widehat {AOB}\) nên \(\widehat {AOC} = {60^0}\). Mà OACB là hình thoi nên tam giác AOC đều. Suy ra OA = OC. Vậy cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là 100N.
Câu b:
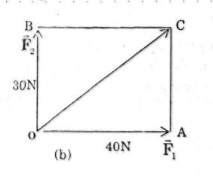
Đặt \(\overrightarrow {OA} = {\overrightarrow F _1},\overrightarrow {OB} = \overrightarrow {{F_2}} \). C là đỉnh thứ tư của hình bình hành OABC.
Do góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng 900 suy ra tứ giác OABC là hình chữ nhật.
\( \Rightarrow OC = \sqrt {O{A^2} + O{B^2}} = \sqrt {{{40}^2} + {{30}^2}} = 50N\)
Ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Vậy cường độ tổng hợp lực của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là 50N.
Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Chương 1 Bài 2 Tổng của hai vectơ với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.
Tư liệu nổi bật tuần
- Xem thêm







