Giải Lý 10 SGK nâng cao Chương 1 Bài 5 Phương trình chuyển động thẳng biến đổi đều

Chọn câu sai

Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu :

A . a > 0 và v₀ > 0

B . a > 0  và v₀ = 0

C . a < 0 và v₀ > 0

D . a < 0 và v₀ = 0

Hướng dẫn giải:

Ta có: \(\left\{ \begin{array}{l} a < 0\\ {v_0} > 0 \end{array} \right. \Rightarrow a.{v_0} < 0\)

→ Lúc đầu chuyển động chậm dần đều, vận tốc giảm dần về O và đổi dấu, từ đây a.v > 0 nên chuyển động là nhanh dần đều.

Chọn đáp án C.

Một chất điểm chuyển động dọc theo trục Ox, theo phương trình \(x = 2t + 3{t^2}\) , trong đó x tính bằng mét, t tính bằng giây.

a) Hãy xác định gia tốc của chất điểm.

b) Tìm tọa độ và vận tốc tức thời của chất điểm lúc t = 3s

Hướng dẫn giải:

\(x = 2t + 3{t^2}(s;m)\)

a) Ta có: \(\frac{a}{2} = 3 \Rightarrow a = 6\left( {m/{s^2}} \right)\)

b) Tại t = 3s , ta có:

\(\begin{array}{l} x = 2.3 + {3.3^2} = 33\left( m \right)\\ v = {v_0} + at = 2 + 6.3 = 20\left( {m/s} \right) \end{array}\)

Vận tốc của một chất điểm chuyển động dọc theo trục Ox cho bởi hệ thức v = (15 – 8t) m/s. Hãy xác định gia tốc, vận tốc của chất điểm lúc t = 2s và vận tốc trung bình của chất điểm trong khoảng thời gian từ t = 0s đến t = 2s.

Hướng dẫn giải:

Ta có: v = 15 – 8t (m/s), a = -8\(m/{s^2}\)

Tại t = 2 (s) có v = 15 – 8.2 = -1 (m/s)

Vận tốc trung bình trong khoảng thời gian từ t = 0s đến t = 2s:

\({\left\{ \begin{array}{l} {\rm{\Delta }}t = t - {t_0} = 2 - 0 = 2\left( s \right)\\ {v_{tb}} = \frac{{{v_0} + v}}{2} = \frac{{15 + \left( { - 1} \right)}}{2} = 7\left( {m/s} \right) \end{array} \right.}\)

Một ô tô đang chuyển động với vận tốc không đổi 30m/s. Đến chân một con dốc, đột nhiên máy ngừng hoạt động và ô tô theo đà đi lên dốc. Nó luôn chịu một gia tốc ngược chiều vận tốc đầu bằng 2m/s² trong suốt quá trình lên dốc và xuống dốc.

a) Viết phương trình chuyển động của ô tô, lấy gốc tọa độ x = 0 và gốc thời gian t = 0 lúc xe ở vị trí chân dốc.

b) Tính quãng đường xa nhất theo sườn dốc mà ô tô có thể lên được.

c) Tính thời gian đi hết quãng đường đó.

d) Tính vận tốc của ô tô sau 20s. Lúc đó ô tô chuyển động theo chiều nào?

Hướng dẫn giải:

a)

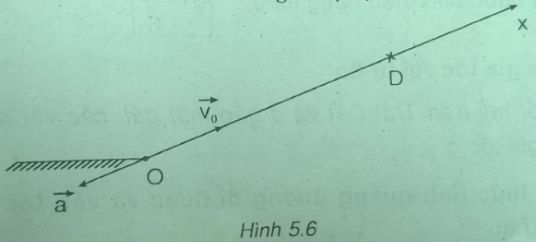
Chọn gốc tọa độ O tại chân dốc, chiều dương hướng lên.

Gốc thời gian là lúc bắt đầu lên dốc thì các giá trị đại số:

v₀ = 30 (m/s); a = -2 (m/s²); x₀ = 0 ( \(\overrightarrow {{v_0}} \) cùng chiều dương nên v₀ > 0; \(\overrightarrow {{a_0}} \) ngược chiều dương nên a < 0

Phương trình chuyển động của xe:

\(x = 30t - {t^2}{\mkern 1mu} {\mkern 1mu} \left( {s;{\mkern 1mu} m} \right)\)

b)Vì a.v₀ < 0 → xe chuyển động chậm dần đều, lên tới điểm D rồi đổi chiều, chuyển động nhanh dần đều xuống:

Tại D ta có:

\(v = 0 \Rightarrow {\rm{\Delta }}x = \frac{{ - v_0^2}}{{2{\rm{a}}}} = \frac{{ - {{30}^2}}}{{2\left( { - 2} \right)}} = 225\left( m \right)\)

Quãng đường xa nhất OD = |∆x| = 225 (m)

c) Thời gian để đi hết quãng đường là:

\(\begin{array}{l} v = {v_0} + at\\ \Rightarrow t = \frac{{v - {v_0}}}{a} = \frac{{ - {v_0}}}{a} = \frac{{ - 30}}{{ - 2}} = 15\left( s \right) \end{array}\)$$

d) Tại t = 20 (s) có: v = 30 – 2.20 = -10 (m/s)

                                v < 0 ⇔ lúc này xe đang xuống dốc.