Bài tập 55 trang 96 SGK Toán 8 Tập 1

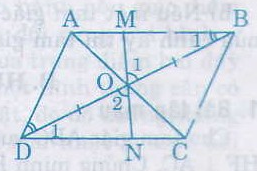
Vì \( ABCD\) là hình bình hành có O là giao điểm hai đường chéo (giả thiết).

\( \Rightarrow AB//DC\) và \(BO=DO\) (tính chất hình bình hành) 

\( \Rightarrow\) \(\widehat{B_{1}} = \widehat{D_{1}}\) (so le trong)

Xét \(\Delta BOM\) và \(\Delta DON\) có:

 \(\widehat{B_{1}} = \widehat{D_{1}}\) (chứng minh trên)

 \(BO = DO\) (chứng minh trên)

 \(\widehat{O_{1}} = \widehat{O_{2}}\) (đối đỉnh) 

\( \Rightarrow\) \( ∆BOM = ∆DON (g.c.g)\)

\( \Rightarrow\) \(OM = ON\) (hai cạnh tương ứng).

\( \Rightarrow\) \(O\) là trung điểm của \(MN\) (dấu hiệu nhận biết trung điểm)

\( \Rightarrow\) \(M \) đối xứng với \(N\) qua \(O\).

-- Mod Toán 8 HỌC247