Bài tập 98 trang 92 SBT Toán 8 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Lời giải chi tiết

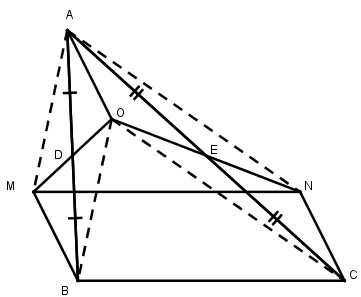
Xét tứ giác AOBM:

DA = DB (gt)

DO = DM (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

⇒ BM // AO và BM = AO (1)

Xét tứ giác AOCN:

EA = EC (gt)

EO = EN (định nghĩa đối xứng tâm)

Suy ra: Tứ giác AOCN là hình bình hành ( vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

⇒ CN // AO và CN = AO (2)

Từ (1) và (2) suy ra: BM // CN và BM = CN

Vậy : Tứ giác BMNC là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)

-- Mod Toán 8 HỌC247