Bài tập 5.2 trang 163 SBT Toán 8 Tập 1
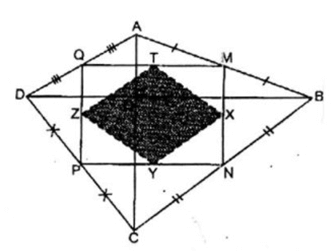
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Biết AC = 6cm, BD = 8cm. Gọi M, N, P, Q theo thứ tự là trung điểm các cạnh AB, BC, CD, DA. Gọi X, Y, Z, T theo thứ tự là trung điểm các cạnh MN, NP, PQ, QM.
a) Chứng minh rằng MNPQ là hình chữ nhật.
b) Tính diện tích của tứ giác XYZT.
Hướng dẫn giải chi tiết
a) Trong ΔABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của ΔABD.
⇒ MQ // BD và MQ = \(\frac{1}{2}\) BD (tính chất đường trung bình của tam giác) (1)
Trong ΔCBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của ΔCBD
⇒ NP // BD và NP = \(\frac{1}{2}\) BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong ΔABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 900
Vậy tứ giác MNPQ là hình chữ nhật.
b) Kẻ đường chéo MP và NQ
Trong ΔMNP ta có:
X là trung điểm của MN
Y là trung điểm của NP
nên XY là đường trung bình của ΔMNP
⇒ XY // MP và XY = \(\frac{1}{2}\) MP (tính chất đường trung bình của tam giác) (3)
Trong ΔQMP ta có:
T là trung điểm của QM
Z là trung điểm của QP
nên TZ là đường trung bình của ΔQMP
⇒ TZ // MP và TZ = \(\frac{1}{2}\) MP (tính chất đường trung bình của tam giác) (4)
Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.
Trong ΔMNQ ta có XT là đường trung bình
⇒ XT = \(\frac{1}{2}\) QN (tính chất đường trung bình của tam giác)
Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ
Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi
SXYZT = \(\frac{1}{2}\) XZ. TY
mà XZ = MQ = \(\frac{1}{2}\) BD = \(\frac{1}{2}\). 8 = 4 (cm);
TY = MN = \(\frac{1}{2}\) AC = \(\frac{1}{2}\) .6 =3 (cm)
Vậy: SXYZT = \(\frac{1}{2}\). 3. 4 = 6 (cm2)
-- Mod Toán 8 HỌC247
-


Bài 44 trang 163 sách bài tập toán 8
bởi Sam sung
 30/12/2019
Bài 44 (Sách bài tập - trang 163)
30/12/2019
Bài 44 (Sách bài tập - trang 163)Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi đó ?
Theo dõi (0) 1 Trả lời -


Bài 43 trang 163 sách bài tập toán 8
bởi Phạm Khánh Ngọc
 30/12/2019
Bài 43 (Sách bài tập - trang 163)
30/12/2019
Bài 43 (Sách bài tập - trang 163)Tính diện tích hình thoi, biết cạnh của nó dài 6,2 cm và một trong các góc của nó có số đo là \(30^0\) ?
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 46 trang 163 SBT Toán 8 Tập 1
Bài tập 5.1 trang 163 SBT Toán 8 Tập 1
Bài tập 5.3 trang 163 SBT Toán 8 Tập 1
Bài tập 42 trang 162 SBT Toán 8 Tập 1
Bài tập 43 trang 163 SBT Toán 8 Tập 1
Bài tập 44 trang 163 SBT Toán 8 Tập 1
Bài tập 45 trang 163 SBT Toán 8 Tập 1
Bài tập 46 trang 163 SBT Toán 8 Tập 1
Bài tập 5.1 trang 163 SBT Toán 8 Tập 1