Giải bài 25 tr 30 sách BT Toán lớp 8 Tập 1
Theo định nghĩa của phép trừ, khi viết
\({A \over B} - {C \over D} - {E \over F}\) có nghĩa là \({A \over B} + {{ - C} \over D} + {{ - E} \over F}\)
Áp dụng điều này để làm các phép tính sau :
a. \({1 \over {3x - 2}} - {1 \over {3x + 2}} - {{3x - 6} \over {4 - 9{x^2}}}\)
b. \({{18} \over {\left( {x - 3} \right)\left( {{x^2} - 9} \right)}} - {3 \over {{x^2} - 6x + 9}} - {x \over {{x^2} - 9}}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng quy tắc trừ các phân thức đại số:
\(\displaystyle{A \over B} - {C \over D} - {E \over F}\) có nghĩa là \(\displaystyle{A \over B} + {{ - C} \over D} + {{ - E} \over F}\)
Từ đó quy đồng mẫu thức rồi đưa về phép cộng các phân thức cùng mẫu.
Lời giải chi tiết
a. \({1 \over {3x - 2}} - {1 \over {3x + 2}} - {{3x - 6} \over {4 - 9{x^2}}}\)\( = {1 \over {3x - 2}} - {1 \over {3x + 2}} + {{3x - 6} \over {\left( {3x + 2} \right)\left( {3x - 2} \right)}}\)
\(\eqalign{ & = {{3x + 2} \over {\left( {3x + 2} \right)\left( {3x - 2} \right)}} + {{ - \left( {3x - 2} \right)} \over {\left( {3x + 2} \right)\left( {3x - 2} \right)}} + {{3x - 6} \over {\left( {3x + 2} \right)\left( {3x - 2} \right)}} \cr & = {{3x + 2 - 3x + 2 + 3x - 6} \over {\left( {3x + 2} \right)\left( {3x - 2} \right)}} = {{3x - 2} \over {\left( {3x + 2} \right)\left( {3x - 2} \right)}} = {1 \over {3x + 2}} \cr} \)
b. \({{18} \over {\left( {x - 3} \right)\left( {{x^2} - 9} \right)}} - {3 \over {{x^2} - 6x + 9}} - {x \over {{x^2} - 9}}\)\( = {{18} \over {{{\left( {x - 3} \right)}^2}\left( {x + 3} \right)}} + {{ - 3} \over {{{\left( {x - 3} \right)}^2}}} + {{ - x} \over {\left( {x + 3} \right)\left( {x - 3} \right)}}\)
\(\eqalign{ & = {{18} \over {{{\left( {x - 3} \right)}^2}\left( {x + 3} \right)}} + {{ - 3\left( {x + 3} \right)} \over {{{\left( {x - 3} \right)}^2}\left( {x + 3} \right)}} + {{ - x\left( {x - 3} \right)} \over {{{\left( {x - 3} \right)}^2}\left( {x + 3} \right)}} = {{18 - 3x - 9 - {x^2} + 3x} \over {{{\left( {x - 3} \right)}^2}\left( {x + 3} \right)}} \cr & = {{9 - {x^2}} \over {\left( {3 - {x^2}} \right)\left( {x + 3} \right)}} = {{\left( {3 - x} \right)\left( {3 + x} \right)} \over {\left( {3 - {x^2}} \right)\left( {x + 3} \right)}} = {1 \over {3 - x}} \cr} \)
-- Mod Toán 8 HỌC247
-


Tính: \( -\dfrac{x^{2}+2}{1-5x}\)
bởi Trần Thị Trang
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Thực hiện phép tính: \(\dfrac{{x + 2}}{{x - 1}} - \dfrac{{x - 9}}{{1 - x}} - \dfrac{{x - 9}}{{1 - x}}\)
bởi Bao Chau
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Làm tính trừ phân thức: \(\dfrac{{x + 3}}{{{x^2} - 1}} - \dfrac{{x + 1}}{{{x^2} - x}}\)
bởi Phan Thị Trinh
 03/02/2021
Theo dõi (0) 1 Trả lời
03/02/2021
Theo dõi (0) 1 Trả lời -


Tìm phân thức đối của \(\dfrac{{1 - x}}{x}\)
bởi Lê Tấn Thanh
 02/02/2021
Theo dõi (0) 1 Trả lời
02/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính (x^2-9)/(2x+6):(3-x)/2
bởi Giang Hoàng Thị
 13/04/2020
13/04/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức x-1/x+1 - x+1/x-1 +4/x^2-1
bởi Vy Bùi
 27/02/2020
27/02/2020
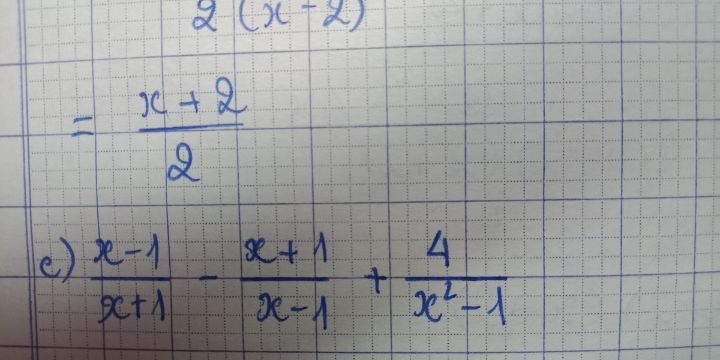 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





