Giải bài 16 tr 28 sách BT Toán lớp 8 Tập 1
Cho hai phân thức \({1 \over {{x^2} + 7x - 15}}\) và \({2 \over {{x^2} - 2x - 3}}\)
Chứng tỏ rằng có thể chọn đa thức \({x^3} - 7{x^2} + 7x + 15\) làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Thực hiện phép chia đa thức \({x^3} - 7{x^2} + 7x + 15\) cho hai đa thức \({{x^2} - 4x - 5}\) và \({{x^2} - 2x - 3}\). Nếu các phép chia đều là phép chia hết thì đa thức \({x^3} - 7{x^2} + 7x + 15\) là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.
Lời giải chi tiết
Ta có:
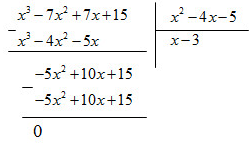
Suy ra: \({x^3} - 7{x^2} + 7x + 15 \)\(\,= \left( {{x^2} - 4x - 5} \right)\left( {x - 3} \right)\)
Suy ra: \({x^3} - 7{x^2} + 7x + 15 \)\(\,= \left( {{x^2} - 2x - 3} \right)\left( {x - 5} \right)\)
Vậy đa thức \({x^3} - 7{x^2} + 7x + 15\) là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho.
* Quy đồng:
\(\displaystyle {1 \over {{x^2} - 4x - 5}}\)
\(\displaystyle= {{1.\left( {x - 3} \right)} \over {\left( {{x^2} - 4x - 5} \right).\left( {x - 3} \right)}}\)
\(\displaystyle= {{x - 3} \over {{x^3} - 7{x^2} + 7x + 15}}\)
\(\displaystyle{2 \over {{x^2} - 2x - 3}} \)
\(\displaystyle= {{2.\left( {x - 5} \right)} \over {\left( {{x^2} - 2x - 3} \right)\left( {x - 5} \right)}} \)
\(\displaystyle= {{2\left( {x - 5} \right)} \over {{x^3} - 7{x^2} + 7x + 15}} \)
-- Mod Toán 8 HỌC247
-
Quy đồng mẫu thức các phân thức 3x/2x+4 và x+3/x^2-4
bởi Lê Chí Thiện
25/12/2018
Quy đồng mẫu thức các phân thức:
a,\(\dfrac{3x}{2x+4}\)và \(\dfrac{x+3}{x^2-4}\)
Theo dõi (0) 2 Trả lời -
Quy đồng mẫu thức các phân thức 2x/x^2-8x+16, x/3x^2-12x
bởi Quế Anh
25/12/2018
Quy đồng mẫu thức các phân thức:
a,\(\dfrac{2x}{x^2-8x+16}\),\(\dfrac{x}{3x^2-12x}\)
Theo dõi (0) 1 Trả lời -
Quy đồng mẫu thức các phân thức:
a,\(\dfrac{5}{x^5y^3}\),\(\dfrac{7}{12x^3y^4}\)
Theo dõi (0) 1 Trả lời -
quy đồng mẫu phân thức sau
\(\dfrac{4x^2-3x+5}{x^3-1}\) , \(\dfrac{1-2x}{x^2+x+1}\) và -2
Theo dõi (0) 1 Trả lời -
Quy đồng x+5/x^2+4x+4 và x/3x+6
bởi Bánh Mì
25/12/2018
quy đồng mẫu thức hai phân thức sau
\(\dfrac{x+5}{x^2+4x+4}và\dfrac{x}{3x+6}\)
Theo dõi (0) 1 Trả lời -
Quy đồng các phân thức 7x-1/2x^2+6x; 3-2x/x^2-9
bởi Lê Tấn Vũ
25/12/2018
Quy đồng mẫu các phân thức:
1) 7x-1/2x^2+6x; 3-2x/x^2-9
2) 2x-1/x-x^2; x+1/2-4x+2x^2
3) x-1/x^3+1; 2x/x^2-x+1; 2/x+1
4) 7/5x; 4/x-2y; x-y/8y^2-2x^2
5) x/x^3-1; x+1/x^2-x; x-1/x^2+x+1
6) x/x^2-2ax+a^2; x+a/x^2-axTheo dõi (0) 1 Trả lời -
Tìm ĐKXĐ của P=3x^2 +6x+12/x^3-8
bởi Nguyễn Trà Giang
30/01/2019
bài tập
Cho biểu thức : P=3x^2 +6x+12 phần x^3-8
a) Tìm điều kiện xác định P
b) rút gọn biểu thức P .
Theo dõi (0) 1 Trả lời -
Rút gọn x^2-2x/x^2-4
bởi hồng trang
30/01/2019
bài 1 : rút gọn các phân thức sau
a, \(\dfrac{x^2-2x}{x^2-4}\)
b, \(\dfrac{x^2+5x+4}{x^2-1}\)
c,\(\dfrac{x^4+4}{x\left(x^2+2\right)-2x^2-\left(x-1\right)^2-1}\)
bài 2 : rút gọn các biểu thức sau.
a,\(\left(\right)\dfrac{2x+1}{2x-1}-\dfrac{2x-1}{2x+1}\left(\right):\dfrac{4x}{10x-5}\)
b, \(\left(\dfrac{1}{x^2+x}-\dfrac{2-x}{x+1}\right):\left(\dfrac{1}{x}+x-2\right)\)
c, \(\left(\dfrac{5x+2}{x^2-10x}\dfrac{5x-2}{x^2+10x}\right)\times\dfrac{x^2-100}{x^2+4}\)
Theo dõi (0) 1 Trả lời -
Quy đồng 5x^2/x^2+5x+6, 2x+3/x^2+7x+10, -5
bởi Nguyễn Thị An
25/12/2018
QUy đồng
\(\dfrac{5x^2}{x^2+5x+6};\dfrac{2x+3}{x^2+7x+10};-5\)
Theo dõi (0) 1 Trả lời -
Cho các phân thức:
\(\dfrac{1}{x-2};\dfrac{15}{2x-1};\dfrac{x-5}{x-2}\)
a) Tìm x nguyên để các phân thức đó có giá trị nguyên
b) Quy đồng mẫu thức các phân thức đó
Theo dõi (0) 1 Trả lời
