Giải bài 15 tr 28 sách BT Toán lớp 8 Tập 1
Cho đa thức B \( = 2{x^3} + 3{x^2} - 29x + 30\) và hai phân thức
\({x \over {2{x^2} + 7x - 15}}\), \({{x + 2} \over {{x^2} + 3x - 10}}\)
a. Chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho.
b. Quy đồng mẫu thức của hai phân thức đã cho.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng quy tắc chia hai đa thức một biến.
Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung
- Tìm nhân tử phụ của mỗi mẫu thức.
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Lời giải chi tiết
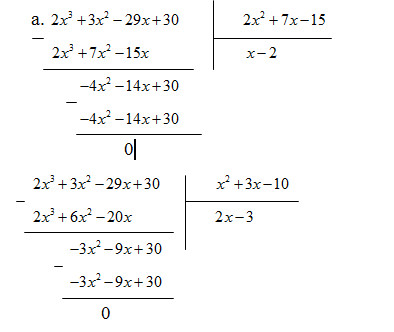
b. MTC = \(2{x^3} + 3{x^2} - 29x + 30\)
\(\eqalign{ & {x \over {2{x^2} + 7x - 15}} = {{x\left( {x - 2} \right)} \over {\left( {2{x^2} + 7x - 15} \right)\left( {x - 2} \right)}} = {{{x^2} - 2x} \over {2{x^3} + 3{x^2} - 29x + 30}} \cr & {{x + 2} \over {{x^2} + 3x - 10}} = {{\left( {x + 2} \right)\left( {2x - 3} \right)} \over {\left( {{x^2} + 3x - 10} \right)\left( {2x - 3} \right)}} = {{\left( {x + 2} \right)\left( {x - 3} \right)} \over {2{x^3} + 3{x^2} - 29x + 30}} \cr} \)
-- Mod Toán 8 HỌC247
-


a) Quy đồng mẫu các phân thức sau đây : 5/x^5*y^3 và 7/12*x^3*y^4
Theo dõi (0) 0 Trả lời -


Quy đồng các phân thức
bởi Bé'ss Nấm'ss
 15/11/2019
15/11/2019
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Thực hiện phép tính x+1/1-x+x^2-2/1-x+2x^2-x/x-1
bởi Ban Mai
 30/01/2019
30/01/2019
1.Thực hiện phép tính
a)\(\dfrac{x+1}{1-x}+\dfrac{x^2-2}{1-x}+\dfrac{2x^2-x}{x-1}\)
b)\(\dfrac{1}{x-1}+\dfrac{2x}{x^2+x+1}+\dfrac{2x-3x^2}{x^3-1}\)
c)\(\dfrac{1}{x^2+4x+4}+\dfrac{-1}{x^2-4x+4}+\dfrac{x}{x^2-4}\)
d)\(\dfrac{1}{x\left(x-y\right)\left(x-z\right)}+\dfrac{1}{y\left(y-x\right)\left(y-z\right)}+\dfrac{1}{z\left(z-x\right)\left(z-y\right)}\)
e)\(\dfrac{yz}{\left(x-y\right)\left(x-z\right)}+\dfrac{xz}{\left(y-x\right)\left(y-z\right)}+\dfrac{xy}{\left(z-x\right)\left(z-y\right)}\)
Các bạn làm giùm mik với nhé chiều nay mik đi hc rùi


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh 4x^2-4x-1 > 0
bởi Choco Choco
 25/12/2018
25/12/2018
\(4x^2-4x-1>0\)
Theo dõi (0) 1 Trả lời -


Tính 2y+x/2y^2-xy+8x/x^2-4y^2+2y-x/2y^2+xy
bởi Thiên Mai
 30/01/2019
30/01/2019
\(\dfrac{2y+x}{2y^{2^{ }}-xy}\)+\(\dfrac{8x}{x^{2^{ }}-4y^2}\)+\(\dfrac{2y-x}{2y^{2^{ }}+xy}\)
Theo dõi (0) 1 Trả lời -


Tìm mẫu chung của phân thức 2/6x^2yz và 5/4xy^3
bởi Thanh Nguyên
 16/12/2019
16/12/2019
?1 cho hai phân thức \(\dfrac{2}{6x^2yz}và\)\(\dfrac{5}{4xy^3}\) có thể chọn mẫu thức chung là 12x2y3z hoặc 24x3y4z hay ko ? nếu được thì mẫu chung nào đợn giản hơn
?2 quy đồng mẫu 2 phân thức \(\dfrac{3}{x^2-5x}và\dfrac{5}{2x-10}\)
?3 quy đồng mẫu hai phân thức \(\dfrac{3}{x^2-5x};\dfrac{-5}{10-2x}\)Theo dõi (0) 1 Trả lời -


Tìm x để 4x-4/2x^2-2 có giá trị bằng 2
bởi Nguyễn Hoài Thương
 25/12/2018
25/12/2018
bài 1:CHO PHÂN THỨC :4x-4/2x2-2
a) Tìm giá trị của x để phân thức có giá trị bằng -2
b) Tìm giá trị của x để phân thức có giá trị là số nguyên
Bài 2 tương tự bài 1 nhưng là phân thức 3x+3 / x2-1
<GIÚP VỚI ĐANG CẦN GẤP>
Theo dõi (0) 1 Trả lời -


Quy đồng các phân thức x-1/x^3+1, 2x/x^2-x+1, 2/x+1
bởi Bo Bo
 30/01/2019
30/01/2019
Quy đồng mẫu thức các phân thức:
a,\(\dfrac{x-1}{x^3+1}\),\(\dfrac{2x}{x^2-x+1}\),\(\dfrac{2}{x+1}\)
Theo dõi (0) 1 Trả lời -


Quy đồng mẫu thức các phân thức:
\(\dfrac{4x^2-3x+5}{x^3-1}\),-2,\(\dfrac{1-2x}{x^2+x+1}\)
Theo dõi (0) 1 Trả lời -


Quy đồng mẫu thức các phân thức 1/x+2, 8/2x-x^2
bởi Mai Thuy
 25/12/2018
25/12/2018
Quy đồng mẫu thức các phân thức:
a,\(\dfrac{1}{x+2}\),\(\dfrac{8}{2x-x^2}\)
Theo dõi (0) 1 Trả lời





