Giải bài 7 trang 87 SGK Toán 7 Chân trời sáng tạo tập 1
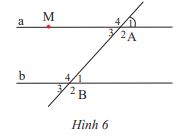
Cho Hình 6, biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = 50^\circ \)
a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.
b) Tính số đo của \(\widehat {{A_3}},\widehat {{B_3}}\)
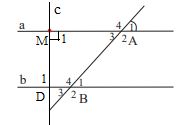
c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c \( \bot \) b.
Hướng dẫn giải chi tiết Bài 7
Phương pháp giải
*Sử dụng tính chất của 2 đường thẳng song song:
Một đường thẳng cắt hai đường thẳng song song thì:
+ 2 góc so le trong bằng nhau
+ 2 góc đồng vị bằng nhau
*2 góc đối đỉnh thì bằng nhau
Lời giải chi tiết
a) Các cặp góc so le trong là: \(\widehat {{A_3}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_4}}\)
Các cặp góc đồng vị là : \(\widehat {{A_1}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_2}};\widehat {{A_3}} = \widehat {{B_3}};\widehat {{A_4}} = \widehat {{B_4}}\)
b) Vì \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 50^\circ \) nên \(\widehat {{A_3}} = 50^\circ \)
Vì a // b nên \(\widehat {{A_3}} = \widehat {{B_3}}\)( 2 góc đồng vị), mà \(\widehat {{A_3}} = 50^\circ \) nên \(\widehat {{B_3}} = 50^\circ \)
c) Gọi c cắt b tại D
Vì a // b nên \(\widehat {{M_1}} = \widehat {{D_1}}\) ( 2 góc so le trong), mà \(\widehat {{M_1}} = 90^\circ \Rightarrow \widehat {{D_1}} = 90^\circ \)
Vậy c \( \bot \) b.
Chú ý: Ta có định lí: Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng song song vói đường thẳng còn lại
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 5 trang 87 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 87 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 87 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 87 SGK Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 87 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 12 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 13 trang 88 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST
Giải bài 14 trang 89 SBT Toán 7 Chân trời sáng tạo tập 1 - CTST