Giải bài 4.20 trang 58 SBT Toán 7 Kết nối tri thức tập 1
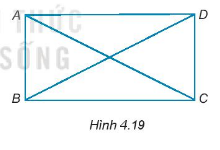
Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (H.4.19)
a) Chứng minh \(\Delta ABD = \Delta DCA;\Delta ADC = \Delta BCD\).
b) Bằng cách tính số đo góc ADC, hãy cho biết ABCD có phải là hình chữ nhật không.
Hướng dẫn giải chi tiết
Phương pháp giải:
a) Chỉ ra các cạnh tương ứng bằng nhau.
b)
-Chứng minh \(\widehat {DAB} = \widehat {ADC}\)
-Chứng minh \(\widehat {ADC} = {90^0}\).
Lời giải chi tiết:
a)
Xét \(\Delta ABD\)và \(\Delta DCA\)có:
AB = DC (2 cạnh đối của hình bình hành)
BD = CA (gt)
AD: Cạnh chung
\( \Rightarrow \Delta ABD = \Delta DCA\left( {c - c - c} \right)\)
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC (2 cạnh đối của hình bình hành)
AC = BD (gt)
DC: Cạnh chung
\( \Rightarrow \Delta ADC = \Delta BCD\left( {c - c - c} \right)\)
b)
Ta có: \(\Delta ABD = \Delta BCD\left( {cmt} \right) \Rightarrow \widehat {DAB} = \widehat {ADC}\) (góc tương ứng).
Mặt khác vì ABCD là hình bình hành nên \(\widehat {DAB} + \widehat {ADC} = {180^0} \Rightarrow \widehat {DAB} = \widehat {ADC} = \dfrac{{{{180}^0}}}{2} = {90^0}\)
Hình bình hành ABCD có một góc vuông nên là hình chữ nhật.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





