Giải bài 4.19 trang 58 SBT Toán 7 Kết nối tri thức tập 1
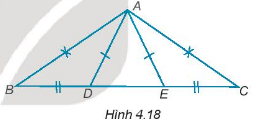
Cho các điểm A, B, C, D, E như hình 4.18, biết rằng AB = AC, AD = AE, BD = CE. Chứng minh rằng \(\widehat {AEB} = \widehat {ADC}\)
Hướng dẫn giải chi tiết
Phương pháp giải:
-Chứng minh \(\Delta AEB\)= \(\Delta ADC\)
Lời giải chi tiết:
Xét \(\Delta AEB\)và \(\Delta ADC\) có:
AB = AC (gt)
AE = AD (gt)
\(\left\{ \begin{array}{l}EB = BD + DE\\CD = CE + DE\end{array} \right. \Rightarrow EB = CD\left( {do\,BD = CE} \right)\)
\( \Rightarrow \Delta AEB = \Delta ADC\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {AEB} = \widehat {ADC}\)(góc tương ứng)
-- Mod Toán 7 HỌC247
Nếu bạn thấy
hướng dẫn giải
Giải bài 4.19 trang 58 SBT Toán 7 Kết nối tri thức tập 1 - KNTT HAY thì click chia sẻ
YOMEDIA
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
