Giải bài 4.18 trang 58 SBT Toán 7 Kết nối tri thức tập 1
Cho hình 4.17, biết rằng AD = BC, AC = BD và \(\widehat {ABD} = {30^0}\), hãy tính số đo của góc DEC.
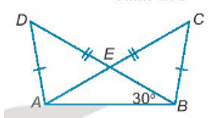
Hướng dẫn giải chi tiết
Phương pháp giải:
-Chứng minh \(\Delta ABC\) = \(\Delta BAD\)
-Tính BAE
-Tính AEB (Tổng 3 góc trong tam giác AEB)
Lời giải chi tiết:
Xét \(\Delta ABC\) và \(\Delta BAD\) có:
AC = BD (gt)
AD = BC (gt)
AB: Cạnh chung
\( \Rightarrow \Delta ABC = \Delta BAD\left( {c - c - c} \right)\\ \Rightarrow \widehat {BAC} = \widehat {ABD}\) ( 2 góc tương ứng)
Mà \(\widehat {ABD} = {30^0}\)
\(\Rightarrow \widehat {BAE} = \widehat {BAC} = \widehat {ABD} = {30^0}\)
Tam giác AEB có: \(\widehat {BAE} + \widehat {AEB} + \widehat {ABE} = {180^0}\) (Tổng 3 góc trong 1 tam giác)
\( \Rightarrow \widehat {AEB} = {180^0} - {30^0} - {30^0} = {120^0}\)
Mà \(\widehat {DEC} = \widehat {AEB}\) (2 góc đối đỉnh).
Do đó, \(\widehat {DEC}= {120^0}\)
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





