HŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 7 Kß║┐t nß╗æi tri thß╗®c B├Āi tß║Łp cuß╗æi chŲ░ŲĪng 3 gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n luyß╗ćn tß╗æt kiß║┐n thß╗®c.
-
Giß║Żi b├Āi 3.32 trang 59 SGK To├Īn 7 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Chß╗®ng minh rß║▒ng: Cho ─æiß╗ām A v├Ā ─æŲ░ß╗Øng thß║│ng d th├¼ c├│ duy nhß║źt ─æŲ░ß╗Øng thß║│ng ─æi qua A v├Ā vu├┤ng g├│c vß╗øi d, tß╗®c l├Ā nß║┐u c├│ hai ─æŲ░ß╗Øng thß║│ng ─æi qua A vu├┤ng g├│c vß╗øi d th├¼ ch├║ng phß║Żi tr├╣ng nhau.
-
Giß║Żi b├Āi 3.33 trang 59 SGK To├Īn 7 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
Vß║Į ba ─æŲ░ß╗Øng thß║│ng ph├ón biß╗ćt a,b,c sao cho a//b, b//c v├Ā hai ─æŲ░ß╗Øng thß║│ng ph├ón biß╗ćt m, n c├╣ng vu├┤ng g├│c vß╗øi a. Hß╗Åi tr├¬n h├¼nh c├│ bao nhi├¬u cß║Ęp ─æŲ░ß╗Øng thß║│ng song song, c├│ bao nhi├¬u cß║Ęp ─æŲ░ß╗Øng thß║│ng vu├┤ng g├│c?
-
Giß║Żi b├Āi 3.34 trang 59 SGK To├Īn 7 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
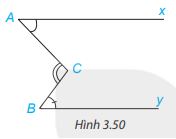
Cho H├¼nh 3.50, trong ─æ├│ hai tia Ax v├Ā By nß║▒m tr├¬n hai ─æŲ░ß╗Øng thß║│ng song song. Chß╗®ng minh rß║▒ng \(\widehat C = \widehat A + \widehat B\)
-
Giß║Żi b├Āi 3.35 trang 59 SGK To├Īn 7 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
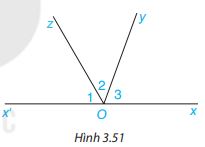
Cho H├¼nh 3.51, trong ─æ├│ Ox v├Ā OxŌĆÖ l├Ā hai tia ─æß╗æi nhau
a) T├Łnh tß╗Ģng sß╗æ ─æo ba g├│c O1, O2, O3 .
Gß╗Żi ├Į: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\), trong ─æ├│ \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {x'Oy}\)
b) Cho \(\widehat {{O_1}} = 60^\circ ,\widehat {{O_2}} = 70^\circ \). T├Łnh \(\widehat {{O_2}}\)
-
Giß║Żi b├Āi 3.36 trang 59 SGK To├Īn 7 K├¬╠üt n├┤╠üi tri thŲ░╠üc tß║Łp 1 - KNTT
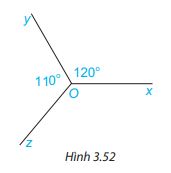
Cho H├¼nh 3.52, biß║┐t \(\widehat {xOy} = 120^\circ ,\widehat {yOz} = 110^\circ \). T├Łnh sß╗æ ─æo g├│c zOx.
Gß╗Żi ├Į: Kß║╗ th├¬m tia ─æß╗æi cß╗¦a tia Oy
-
Giß║Żi C├óu hß╗Åi 1 trang 47 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho hai g├│c kß╗ü b├╣ AOB v├Ā BOC. Tia OM nß║▒m giß╗»a hai tia OB v├Ā OC. Tia ON l├Ā tia ─æß╗æi cß╗¦a tia OM. Khi ─æ├│ cß║Ęp g├│c ─æß╗æi ─æß╗ēnh l├Ā cß║Ęp g├│c n├Āo trong c├Īc cß║Ęp g├│c sau ─æ├óy?
A. \(\widehat {BOM}\) v├Ā \(\widehat {CON}\)
B.\(\widehat {AOB}\) v├Ā \(\widehat {AON}\)
C. \(\widehat {AOM}\) v├Ā \(\widehat {CON}\)
D. \(\widehat {COM}\) v├Ā \(\widehat {CON}\).
-
Giß║Żi C├óu hß╗Åi 2 trang 47 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Trong c├Īc khß║│ng ─æß╗ŗnh sau, khß║│ng ─æß╗ŗnh n├Āo ─æ├║ng?
A. Hai g├│c bß║▒ng nhau th├¼ ─æß╗æi ─æß╗ēnh;
B. Hai g├│c kh├┤ng ─æß╗æi ─æß╗ēnh th├¼ kh├┤ng bß║▒ng nhau;
C. Hai g├│c ─æß╗æi ─æß╗ēnh th├¼ bß║▒ng nhau;
D. Cß║Ż ba khß║│ng ─æß╗ŗnh tr├¬n ─æß╗üu ─æ├║ng.
-
Giß║Żi C├óu hß╗Åi 3 trang 47 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Hai ─æŲ░ß╗Øng thß║│ng cß║»t nhau tß║Īo th├Ānh bß╗æn g├│c kh├Īc g├│c bß║╣t. Biß║┐t sß╗æ ─æo cß╗¦a mß╗Öt trong bß╗æn g├│c ─æ├│ l├Ā \({65^0}\). Khi ─æ├│ sß╗æ ─æo cß╗¦a ba g├│c c├▓n lß║Īi l├Ā:
A.\({65^0};{110^0};{120^0};\)
B. \({65^0};{65^0};{115^0};\)
C. \({115^0};{115^0};{50^0};\)
D. \({65^0};{115^0};{115^0}.\)
-
Giß║Żi C├óu hß╗Åi 4 trang 47 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Hai ─æŲ░ß╗Øng thß║│ng cß║»t nhau tß║Īo th├Ānh bß╗æn g├│c kh├Īc g├│c bß║╣t. Sß╗æ ─æo cß╗¦a bß╗æn g├│c ─æ├│ c├│ thß╗ā l├Ā trŲ░ß╗Øng hß╗Żp n├Āo trong c├Īc trŲ░ß╗Øng hß╗Żp sau ─æ├óy?
A.\({70^0};{70^0};{70^0};{110^0}\)
B. \({60^0};{120^0};{120^0};{120^0};\)
C. \({80^0};{50^0};{130^0};{100^0};\)
D. \({90^0};{90^0};{90^0};{90^0}.\)
-
Giß║Żi C├óu hß╗Åi 5 trang 47 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Hai ─æŲ░ß╗Øng thß║│ng AB v├Ā CD cß║»t nhau tß║Īi O. Cho OM l├Ā tia ph├ón gi├Īc cß╗¦a g├│c BOD v├Ā \(\widehat {BOM} = {30^0}\). Sß╗æ ─æo cß╗¦a g├│c AOC bß║▒ng:
A.\({30^0};\)
B. \({60^0};\)
C. \({120^0};\)
D. Mß╗Öt kß║┐t quß║Ż kh├Īc.
-
Giß║Żi C├óu hß╗Åi 6 trang 48 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho hình 3.29.
a) Cß║Ęp g├│c so le trong l├Ā cß║Ęp g├│c
A.\(\widehat {{M_1}},\widehat {{M_2}};\)
B. \(\widehat {{M_1}},\widehat {{N_1}};\)
C. \(\widehat {{M_1}},\widehat {{N_2}};\)
D. \(\widehat {{M_2}},\widehat {{N_1}}.\)
b) Cß║Ęp g├│c ─æß╗ōng vß╗ŗ l├Ā cß║Ęp g├│c:
A.\(\widehat {{M_1}},\widehat {{M_2}};\)
B. \(\widehat {{M_1}},\widehat {{N_1}};\)
C. \(\widehat {{M_1}},\widehat {{N_2}};\)
D. \(\widehat {{M_2}},\widehat {{N_1}}.\)
-
Giß║Żi C├óu hß╗Åi 7 trang 48 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho h├¼nh 3.30. Cß║Ęp g├│c \(\widehat {{A_1}};\widehat {{B_1}}\) l├Ā cß║Ęp g├│c:
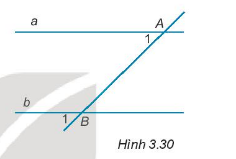
A. So le trong;
B. ─Éß╗æi ─æß╗ēnh;
C. ─Éß╗ōng vß╗ŗ;
D. Cß║Ż ba phŲ░ŲĪng ├Īn tr├¬n ─æß╗üu sai.
-
Giß║Żi C├óu hß╗Åi 8 trang 48 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
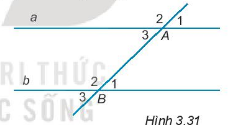
Cho H├¼nh 3.31, ─æŲ░ß╗Øng thß║│ng a song song vß╗øi ─æŲ░ß╗Øng thß║│ng b nß║┐u
A.\(\widehat {{A_1}} = \widehat {{B_2}}\)
B. \(\widehat {{A_2}} = \widehat {{B_3}}\)
C. \(\widehat {{A_3}} = \widehat {{B_2}}\)
D. \(\widehat {{A_3}} = \widehat {{B_1}}\)
-
Giß║Żi C├óu hß╗Åi 9 trang 48 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho Hình 3.32, biết \(a// b\).
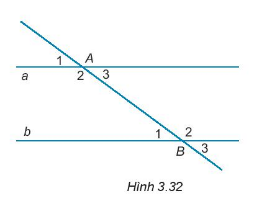
Khß║│ng ─æß╗ŗnh n├Āo sau ─æ├óy l├Ā sai?
A.\(\widehat {{A_1}} > \widehat {{B_1}}\)
B. \(\widehat {{A_2}} = \widehat {{B_2}}\)
C. \(\widehat {{A_3}} = \widehat {{B_1}}\)
D. \(\widehat {{A_3}} = \widehat {{B_3}}\)
-
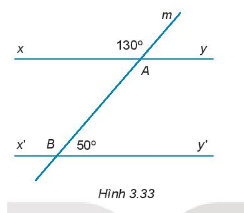
Giß║Żi b├Āi 3.33 trang 49 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho h├¼nh 3.33. H├Ży chß╗®ng minh \(xy\parallel x'y'\)
-
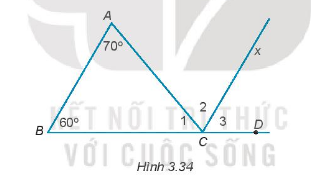
Giß║Żi b├Āi 3.34 trang 49 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho hình 3.34. Biết \(AB\parallel Cx;\widehat A = {70^0};\widehat B = {60^0}.\)
T├Łnh sß╗æ ─æo c├Īc g├│c \(\widehat {{C_1}};\widehat {{C_2}};\widehat {{C_3}}.\)
-
Giß║Żi b├Āi 3.35 trang 49 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho h├¼nh 3.35. Biß║┐t CN l├Ā tia ph├ón gi├Īc cß╗¦a g├│c ACM.
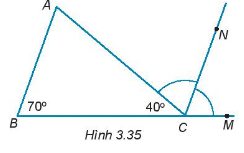
a) Chß╗®ng minh rß║▒ng \(CN//AB\).
b) T├Łnh sß╗æ ─æo cß╗¦a g├│c A.
-
Giß║Żi b├Āi 3.36 trang 50 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Cho h├¼nh 3.36. B├¬n trong g├│c BOD vß║Į tia Ox song song vß╗øi AB. Biß║┐t \(\widehat B = {40^0};\widehat D = {70^0};\widehat {BOD} = {110^0}\).
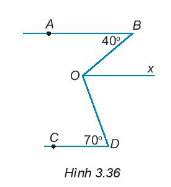
a) T├Łnh sß╗æ ─æo g├│c BOx.
b) Chß╗®ng minh \(Ox// CD;AB// CD.\)
-
Giß║Żi b├Āi 3.37 trang 50 SBT To├Īn 7 Kß║┐t nß╗æi tri thß╗®c tß║Łp 1 - KNTT
Trong hình 3.37 có \(BE// AC,CF// AB\). Biết \(\widehat A = {80^0};\widehat {ABC} = {60^0}\).
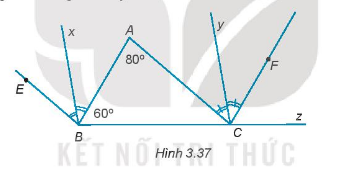
a) Chß╗®ng minh rß║▒ng \(\widehat {ABE} = \widehat {ACF}.\)
b) T├Łnh sß╗æ ─æo cß╗¦a c├Īc g├│c BCF v├Ā ACB.
c) Gß╗Źi Bx, Cy lß║¦n lŲ░ß╗Żt l├Ā tia ph├ón gi├Īc cß╗¦a c├Īc g├│c ABE v├Ā ACF. Chß╗®ng minh rß║▒ng \(Bx// Cy\).