Hướng dẫn Giải bài tập Toán 7 Chân trời sáng tạo Chương 8 Bài 6 Tính chất ba đường trung trực của tam giác giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khám phá 1 trang 71 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
-
Thực hành 1 trang 71 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC.
-
Vận dụng 1 trang 71 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Vẽ ba đường trung trực của tam giác ABC vuông tại A.
-
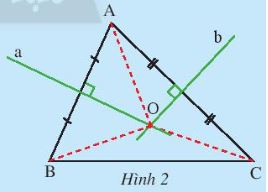
Hoạt động khám phá 2 trang 71 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Gọi O là giao điểm của hai đường trung trực ứng với cạnh AB, AC của tam giác ABC (Hình 2).
- Hãy so sánh độ dài của ba đoạn thẳng OA, OB, OC
- Theo em đường trung trực ứng với cạnh BC có đi qua điểm O hay không?
-
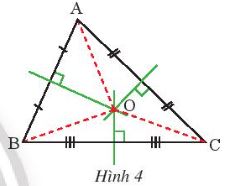
Thực hành 2 trang 72 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Gọi O là giao điểm của ba đường trung trực của tam giác ABC (Hình 4). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không.
-
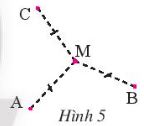
Vận dụng 2 trang 72 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Trên bản đồ qui hoạch một khu dân cư có ba điểm A, B, C (Hình 5). Tìm địa điểm M để xây một trường học sao cho trường học này cách đều ba điểm dân cư đó.
-
Giải bài 1 trang 72 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Vẽ ba tam giác nhọn, vuông, tù
a) Xác định điểm O cách đều ba đỉnh của mỗi tam giác
b) Nêu nhận xét của em về vị trí của điểm O trong mỗi trường hợp.
-
Giải bài 2 trang 72 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC, PO vuông góc với AC.
-
Giải bài 3 trang 72 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (Hình 6). Làm thế nào để các định được bán kính của đĩa cổ này?
-
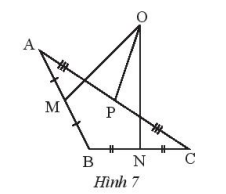
Giải bài 1 trang 57 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Điểm O trong hình 7 có phải là giao điểm của ba đường trung trực của tam giác ABC hay không? Hãy giải thích.
-
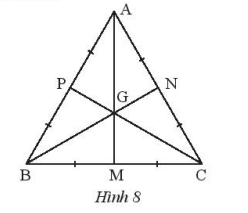
Giải bài 2 trang 57 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác đều ABC và điểm G như trong hình 8. Hãy chứng minh GA = GB = GC.
-
Giải bài 3 trang 58 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có góc A bằng \({120^o}\). Các đường trung trực của AB và Ac lần lượt cắt Bc tại M và N. Tính số đo góc MAN.
-
Giải bài 4 trang 58 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có góc A là góc từ. Các đường trung trực của AB và Ac cắt nhau tại O và lần lượt cắt BC tại E và F. Hãy chứng minh
a) \(\Delta EO{\rm{A}} = \Delta EOB,\Delta F{\rm{O}}A = \Delta F{\rm{O}}C\)
b) Chứng minh rằng AO là tia phân giác của góc EAF.
-
Giải bài 5 trang 58 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có đường trung trực cạnh AC đi qua đỉnh B, chứng minh tam giác ABC là tam giác cân