Giải bài tập Toán 7 Cánh diều Bài 11: Tính chất ba đường phân giác của tam giác

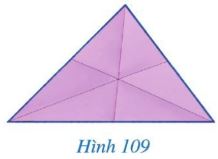
Bạn Ngân gấp một miếng bìa hình tam giác để các nếp gấp tạo thành ba tia phân giác của các góc ở đỉnh của tam giác đó (Hình 109).

Ba nếp gấp đó có đặc điểm gì?

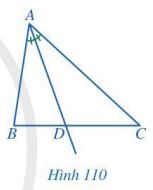
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?

Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.

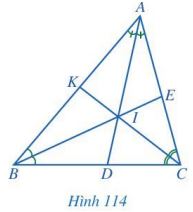
Quan sát các đường phân giác AD, BE, CK của tam giác ABC (Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.

Tìm số đo x trong Hình 115.

Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.

Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.

a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?

b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?

Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:

a) \(\widehat {IAB} + \widehat {IBC} + \widehat {ICA} = 90^\circ \); 

b) \(\widehat {BIC} = 90^\circ  + \dfrac{1}{2}\widehat {BAC}\).

Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.

a) Chứng minh \(\widehat {CBI} > \widehat {ACI}\);      

b) So sánh IB và IC.

Cho tam giác ABC (AB < AC). Trên tia phân giác của góc A, lấy điểm E nằm trong tam giác ABC sao cho E cách đều hai cạnh AB, BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Điểm E không nằm trên tia phân giác của góc B.

b) \(\widehat {EBC} = \widehat {ECB}\).

c) Điểm E cách đều AB, BC, CA.

d) Điểm E nằm trên tia phân giác của góc C.

Cho tam giác ABC có \(\widehat {ABC} + \widehat {ACB} = 2\widehat {BAC}\). Hai tia phân giác của góc B và góc C cắt nhau tại K. Trong các phát biểu sau, phát biểu nào sai?

a) Số đo góc KAC bằng 30°.

b) Số đo góc BAK bằng 25°.

c) Số đo góc BKC bằng 120°.

d) Số đo góc BKC bằng 115°.

Cho tam giác ABC cân tại A có K là trung điểm của đoạn BC. Hai đường phân giác BD và CE cắt nhau tại I. Chứng minh:

a) I cách đều ba cạnh của tam giác ABC;

b) KI là tia phân giác của góc EKD.

Cho tam giác ABC vuông tại C có ˆCAB=60°CAB^=60°, AE là tia phân giác của góc CAB (E ∈ BC). Gọi D là hình chiếu của B trên tia AE, K là hình chiếu của E trên AB. Chứng minh:

a) EB là tia phân giác của góc DEK, EK là tia phân giác của góc BEA;

b) EC = ED = EK.

Cho hai đường thẳng song song a, b và một đường thẳng c (c cắt a tại E, c cắt b tại F). Hai tia phân giác của các góc aEF và bFE cắt nhau tại I. Gọi A, B lần lượt là hình chiếu của I trên các đường thẳng a và b (Hình 52).

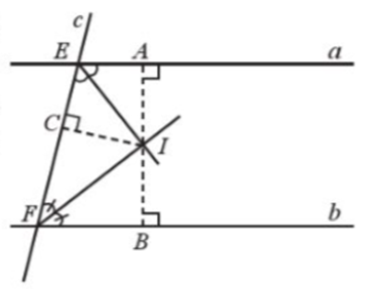
Chứng minh:

a) Tam giác EIF là tam giác vuông;

b) IA = IB.

Cho tam giác ABC cân tại A có M là trung điểm của BC. G là giao điểm của hai trung tuyến BD và CE.

a) Chứng minh: GA, GM, MA lần lượt là tia phân giác của các góc DGE, BGC, EMD.

b) Tìm điều kiện của tam giác ABC để EG là tia phân giác của góc DEM.