Giải bài 1 trang 111 SGK Toán 7 Cánh diều tập 2
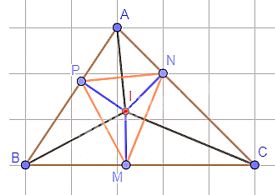
Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?
b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
a) Dựa vào tính chất của ba đường phân giác trong tam giác: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác.
b) Dựa vào chứng minh các cặp tam giác bằng nhau.
Lời giải chi tiết
a) Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Vậy các tam giác IMN, INP, IPM có là tam giác cân tại I.
b)
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông). Suy ra: CN = CM ( 2 cạnh tương ứng).
Vậy tam giác CMN có là tam giác cân.
Tương tự, ta có: AP = AN; BP = BM.
Vậy các tam giác ANP, BPM, CMN có là tam giác cân.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 2 trang 110 SGK Toán 7 Cánh diều tập 2 - CD
Luyện tập 3 trang 111 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 2 trang 111 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 3 trang 111 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 79 trang 92 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 80 trang 92 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 81 trang 92 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 82 trang 92 SBT Toán 7 Cánh diều tập 2 - CD