Giải bài 6.1 tr 111 sách BT Toán lớp 7 Tập 1
Cho hình bs 8 (các đường thẳng \(Er, Dp\) và \(Fq\) song song với nhau). Khi đó, hai đường thẳng \(DE\) và \(DF\) có vuông góc với nhau không? Vì sao?
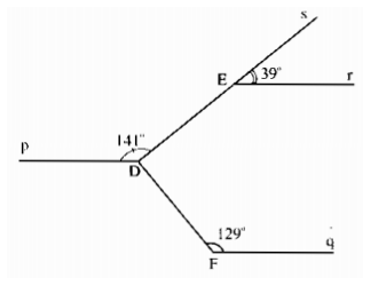
Hướng dẫn giải chi tiết
Hướng dẫn giải
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau, hai góc trong cùng phía bù nhau.
Lời giải chi tiết
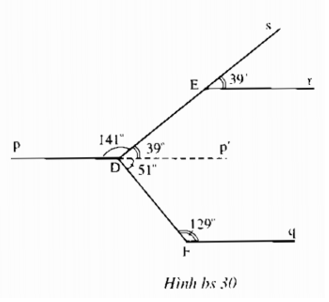
Kẻ thêm \(Dp’ \) là tia đối của tia \(Dp.\)
Khi đó \(Er\) song song với \(pp’\) nên \(\widehat {EDp'} = \widehat {{E_1}} = {39^o}\) (hai góc đồng vị).
\(pp’\) song song với \(Fq\) nên ta có:
\(\widehat {FDp'} + \widehat {{F_1}} = {180^o}\) (hai góc trong cùng phía)
\(\Rightarrow \widehat {FDp'} = {180^o} - \widehat {{F_1}}\)
\(= {180^o} - {129^o} = {51^o}\)
\(\Rightarrow \widehat {EDF} = \widehat {EDp'} + \widehat {FDp'} \)\(\,= {39^o} + {51^o} = {90^o}\)
Vậy hai đường thẳng \(DE\) và \(DF\) vuông góc với nhau.
-- Mod Toán 7 HỌC247
-


Cho tam giác vuông ABC, A = 90, đường cao AH, trung tuyến AM, trên tia đối tia MA lấy điểm D sao cho DM = MA
bởi hà trang
 18/03/2018
18/03/2018
Mn ơi giải hộ mình bài này vs
Cho tam giác vuông ABC: \(\widehat A = {90^0}\), đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E.
Chứng minh: AE = BC.
Theo dõi (0) 1 Trả lời





