Giải bài 6.2 tr 111 sách BT Toán lớp 7 Tập 1
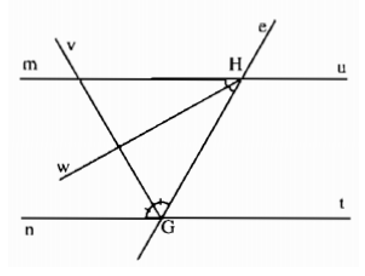
Cho đường thẳng \(e\) cắt hai đường thẳng song song với nhau là \(nt\) và \(mu.\) Biết rằng \(Hw\) là tia phân giác của góc \(mHG\) và \(Gv\) là tia phân giác của góc \(nGH\) (hình bs 9)
Hai đường thẳng \(Gv\) và \(Hw\) có vuông góc với nhau không? Vì sao?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Lời giải chi tiết
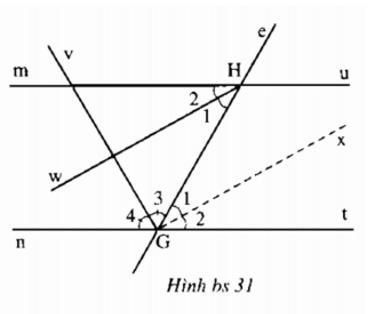
Vẽ tia \(Gx\) là tia phân giác của góc \(HGt.\)
Vì \(mu//nt\) nên \(\widehat {mHG} = \widehat {HGt}\) (hai góc so le trong).
Hơn nữa \(Hw\) và \(Gx\) lần lượt là tia phân giác của \(\widehat {mHG};\,\widehat {HGt}\) nên suy ra \(\widehat {{H_1}} = \widehat {{G_1}} = \dfrac{{\widehat {mHG}}}{2} = \dfrac{{\widehat {HGt}}}{2}\)
Mà \(\widehat {{H_1}} \) và \( \widehat {{G_1}}\) là hai góc ở vị trí so le trong nên \(Hw\) song song với \(Gx.\)
\(\widehat {nGH}\) và \(\widehat {HGt}\) là hai góc kề bù và \(Gv,\; Gx\) lần lượt là tia phân giác của mỗi góc trên nên ta có:
\(\widehat {{G_3}} + \widehat {{G_1}} = \dfrac{{\widehat {nGH}}}{2} + \dfrac{{\widehat {HGt}}}{2} \)\(\,= \dfrac{1}{2}\left( {\widehat {nGH} + \widehat {HGt}} \right) = \dfrac{1}{2}{.180^o} = {90^o}\)
Do đó \(Gv\bot \,Gx\).
Mà \(Gx//Hw\) nên \(Gv\bot\, Hw\).
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





