Hoạt động khám phá 7 trang 71 SGK Toán 11 Chân trời sáng tạo tập 2
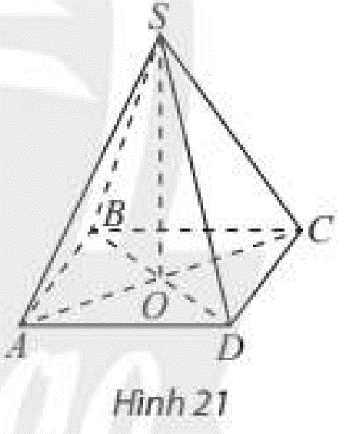
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông với tâm \(O\) và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng \(SO\) có vuông góc với đáy không?
Hướng dẫn giải chi tiết Hoạt động khám phá 7
Phương pháp giải:
Sử dụng định lí: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
Lời giải chi tiết:
Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Thực hành 3 trang 71 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 3 trang 71 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 4 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 8 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





