Bài tập 1 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo
Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD). Cho biết BC = , AB = . Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD)?
Hướng dẫn giải chi tiết Bài tập 1
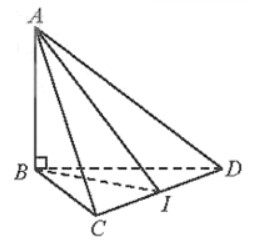
Gọi I là trung điểm của CD.
Ta có: CD ⊥ BI và CD ⊥ AB suy ra CD ⊥ AI.
Ta nhận thấy: CD là giao tuyến của 2 mặt phẳng (ACD) và (BCD);
Mà \(\left\{ \begin{matrix} AI\bot CD,AI\subset (ACD) \\ BI\bot CD,BI\subset (BCD) \\ \end{matrix} \right.\)
Suy ra
Tam giác BCD vuông cân tại B nên
Xét tam giác ABI vuông tại B, ta có:
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là .
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 5 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 2 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





