Hoạt động khám phá 8 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2
Cho hình chóp đều \(S.{A_1}{A_2}{A_3}...{A_6}\). Mặt phẳng \(\left( P \right)\) song song với mặt đáy và cắt các cạnh bên lần lượt tại \({A_1}^\prime ,{A_2}^\prime ,{A_3}^\prime ,...,{A_6}^\prime \).
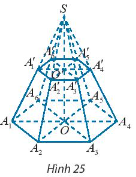
a) Đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) có phải lục giác đều không? Giải thích.
b) Gọi \(O\) và \(O'\) lần lượt là tâm của hai lục giác \({A_1}{A_2}{A_3}...{A_6}\) và \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \). Đường thẳng \(OO'\) có vuông góc với mặt đáy không?
\( \Rightarrow {A_1}^\prime {A_2}^\prime = {A_2}^\prime {A_3}^\prime = {A_3}^\prime {A_4}^\prime = {A_4}^\prime {A_5}^\prime = {A_5}^\prime {A_6}^\prime = {A_6}^\prime {A_1}^\prime \)
Vậy đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) là lục giác đều.
b) Ta có:
\(\left. \begin{array}{l}O' \in {A_1}^\prime {A_4}^\prime \subset \left( {S{A_1}{A_4}} \right)\\O' \in {A_3}^\prime {A_6}^\prime \subset \left( {S{A_3}{A_6}} \right)\\\left( {S{A_1}{A_4}} \right) \cap \left( {S{A_3}{A_6}} \right) = SO\end{array} \right\} \Rightarrow O' \in SO\)
Mà \(S.{A_1}{A_2}{A_3}...{A_6}\) là hình chóp đều \( \Rightarrow SO \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
Vậy \(OO' \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
Hướng dẫn giải chi tiết Hoạt động khám phá 8
Phương pháp giải:
Sử dụng tính chất của hai mặt phẳng song song.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{*{20}{l}}
{\left( P \right)\parallel \left( {{A_1}{A_2}{A_3}...{A_6}} \right)}\\
\begin{array}{l}
\Rightarrow {A_1}^\prime {A_2}^\prime \parallel {A_1}{A_2},\\
{A_2}^\prime {A_3}^\prime \parallel {A_2}{A_3},\\
{A_3}^\prime {A_4}^\prime \parallel {A_3}{A_4},\\
{A_4}^\prime {A_5}^\prime \parallel {A_4}{A_5},\\
{A_5}^\prime {A_6}^\prime \parallel {A_5}{A_6},\\
{A_6}^\prime {A_1}^\prime \parallel {A_6}{A_1}
\end{array}\\
\begin{array}{l}
\Rightarrow \frac{{{A_1}^\prime {A_2}^\prime }}{{{A_1}{A_2}}} = \frac{{{A_2}^\prime {A_3}^\prime }}{{{A_2}{A_3}}}\\
= \frac{{{A_3}^\prime {A_4}^\prime }}{{{A_3}{A_4}}} = \frac{{{A_4}^\prime {A_5}^\prime }}{{{A_4}{A_5}}}\\
= \frac{{{A_5}^\prime {A_6}^\prime }}{{{A_5}{A_6}}} = \frac{{{A_6}^\prime {A_1}^\prime }}{{{A_6}{A_1}}}
\end{array}
\end{array}\)
Mà \({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} = {A_5}{A_6} = {A_6}{A_1}\)
\( \Rightarrow {A_1}^\prime {A_2}^\prime \)\(= {A_2}^\prime {A_3}^\prime\)\( = {A_3}^\prime {A_4}^\prime \)\(= {A_4}^\prime {A_5}^\prime \)\(= {A_5}^\prime {A_6}^\prime\)\( = {A_6}^\prime {A_1}^\prime \)
Vậy đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) là lục giác đều.
b) Ta có:
\(\begin{array}{l}
\left. {\begin{array}{*{20}{l}}
{O' \in {A_1}^\prime {A_4}^\prime \subset \left( {S{A_1}{A_4}} \right)}\\
{O' \in {A_3}^\prime {A_6}^\prime \subset \left( {S{A_3}{A_6}} \right)}\\
{\left( {S{A_1}{A_4}} \right) \cap \left( {S{A_3}{A_6}} \right) = SO}
\end{array}} \right\}\\
\Rightarrow O' \in SO
\end{array}\)
Mà \(S.{A_1}{A_2}{A_3}...{A_6}\) là hình chóp đều \( \Rightarrow SO \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
Vậy \(OO' \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Thực hành 4 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 4 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





