Giải Bài 5 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2
Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ và đường nối tâm hai đáy bằng \(a\). Tính độ dài cạnh bên và đường cao của mỗi mặt bên.
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Sử dụng định lí Pitago.
Lời giải chi tiết
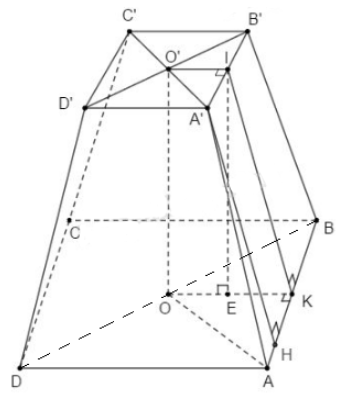
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 3 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





