Hoạt động khám phá 5 trang 68 SGK Toán 11 Chân trời sáng tạo tập 2
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:
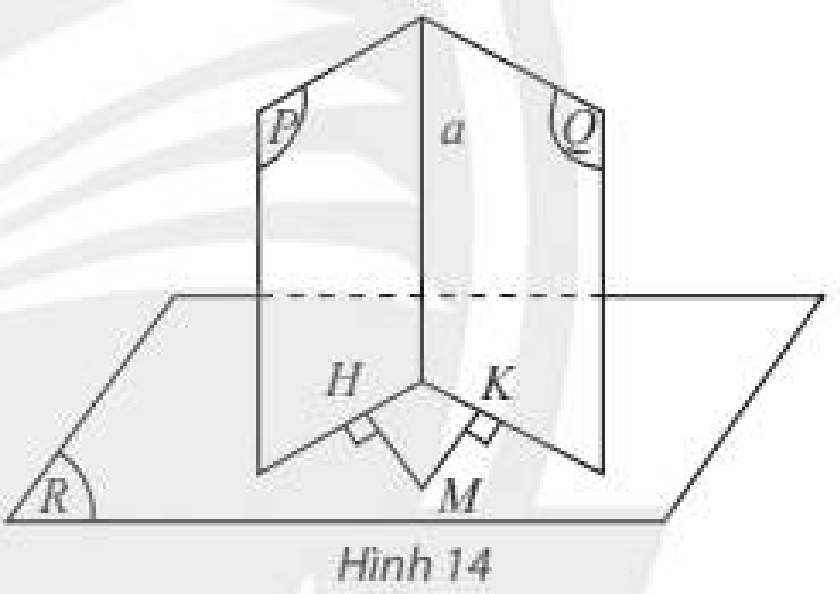
a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?
b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?
Hướng dẫn giải chi tiết Hoạt động khám phá 5
Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Vận dụng 1 trang 67 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 4 trang 67 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 69 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 2 trang 69 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 6 trang 69 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 3 trang 71 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 3 trang 71 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 7 trang 71 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 4 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 8 trang 72 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 5 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 73 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 74 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 61 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 5 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 6 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 7 trang 62 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST





