Hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 8 Bài 4 Hai mặt phẳng vuông góc môn Toán học lớp 11 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động 1 trang 95 SGK Toán 11 Tập 2 Cánh diều - CD
Hai vách ngăn tủ trong Hình 45 gợi nên hình ảnh hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau tạo nên bốn góc nhị diện. Các góc nhị diện đó có phải là những góc nhị diện vuông hay không?

-
Luyện tập 1 trang 95 SGK Toán 11 Tập 2 Cánh diều - CD
Nêu ví dụ trong thực tiễn minh hoạ hình ảnh hai mặt phẳng vuông góc?
-
Hoạt động 2 trang 96 SGK Toán 11 Tập 2 Cánh diều - CD
Nền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) và đường thẳng \(a\) nằm trên mặt phẳng \(\left( P \right)\). Quan sát Hình 48 và cho biết:
a) Vị trí tương đối của đường thẳng \(a\) và mặt phẳng \(\left( Q \right)\);
b) Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có vuông góc với nhau không.

-
Luyện tập 2 trang 97 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(SA \bot \left( {ABCD} \right)\). Chứng minh rằng \(\left( {SAC} \right) \bot \left( {SBD} \right)\)?
-
Hoạt động 3 trang 97 SGK Toán 11 Tập 2 Cánh diều - CD
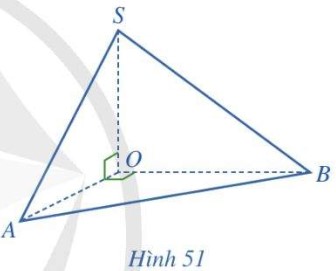
Cho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\), \(\widehat {AOS} = \widehat {AOB} = {90^ \circ }\) (Hình 51).
a) Giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) là đường thẳng nào?
b) \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) hay không?
c) \(SO\) có vuông góc với mặt phẳng \(\left( {AOB} \right)\) hay không?
-
Luyện tập 3 trang 97 SGK Toán 11 Tập 2 Cánh diều - CD
Cho tứ diện \(ABCD\) có \(\left( {ABD} \right) \bot \left( {BCD} \right)\) và \(CD \bot BD\). Chứng minh rằng tam giác \(ACD\) vuông?
-
Hoạt động 4 trang 98 SGK Toán 11 Tập 2 Cánh diều - CD
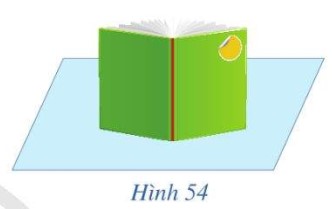
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không?
-
Luyện tập 4 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SC \bot SA\). Chứng minh rằng:
a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\);
b) \(\left( {SBC} \right) \bot \left( {SCA} \right)\);
c) \(\left( {SCA} \right) \bot \left( {SAB} \right)\).
-
Bài 1 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Quan sát ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) ở Hình 57, chỉ ra hai cặp mặt phẳng mà mỗi cặp gồm hai mặt phẳng vuông góc với nhau. Hãy sử dụng kí hiệu để viết những kết quả đó?

-
Bài 2 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Chứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia?
-
Bài 3 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt còn lại.
-
Bài 4 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho?
-
Bài 5 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy, tam giác \(SAB\) vuông cân tại \(S\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng:
a) \(SM \bot \left( {ABCD} \right)\);
b) \(AD \bot \left( {SAB} \right)\);
c) \(\left( {SAD} \right) \bot \left( {SBC} \right)\).
-
Bài 6 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Cho lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh cùng bằng \(a\), hai mặt phẳng \(\left( {A'AB} \right)\) và \(\left( {A'AC} \right)\) cùng vuông góc với \(\left( {ABC} \right)\).
a) Chứng minh rằng \(AA' \bot \left( {ABC} \right)\).
b) Tính số đo góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\).
-
Bài tập 33 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hai mặt phẳng (P), (Q) cắt nhau và đường thẳng a nằm trong (P). Phát biểu nào sau đây là sai?
A. Nếu a ⊥ (Q) thì (P) ⊥ (Q);
B. Nếu a ⊥ (Q) thì a ⊥ b với mọi b ⊂ (Q);
C. Nếu a ⊥ (Q) thì (P) // (Q);
D. Nếu a ⊥ (Q) thì a ⊥ d với d = (P) ⋂ (Q).
-
Bài tập 34 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hai mặt phẳng (P), (Q) vuông góc và cắt nhau theo giao tuyến d, đường thẳng a song song với (P). Phát biểu nào sau đây đúng?
A. Nếu a ⊥ d thì a ⊥ (Q);
B. Nếu a ⊥ d thì a // (Q);
C. Nếu a ⊥ d thì a // b với mọi b ⊂ (Q);
C. Nếu a ⊥ d thì a // c với mọi c // (Q).
-
Bài tập 35 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì:
A. Song song với nhau;
B. Trùng nhau;
C. Không song song với nhau;
D. Song song với nhau hoặc cắt nhau theo giao tuyến vuông góc với mặt phẳng thứ ba.
-
Bài tập 36 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp S.ABCD có hai mặt (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABCD). Khi đó mặt phẳng (ABCD) cùng vuông góc với đường thẳng:
A. SA; B. SB; C. SC; D. SD.
-
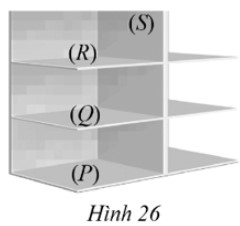
Bài tập 37 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Hình 26 gợi nên hình ảnh một số cặp mặt phẳng vuông góc với nhau. Hãy chỉ ra 2 cặp mặt phẳng vuông góc với nhau?
-
Bài tập 38 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Chứng minh các định lí sau:
a) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
b) Cho một mặt phẳng và một đường thẳng không vuông góc với mặt phẳng đó. Khi đó tồn tại duy nhất một mặt phẳng chứa đường thẳng đã cho và vuông góc với mặt phẳng đã cho.
-
Bài tập 39 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình lăng trụ ABC.A’B’C’ có AA’ ⊥ (ABC), tam giác ABC cân tại A. Gọi M là trung điểm của BC. Chứng minh rằng (MAA’) ⊥ (BCC’B’)?
-
Bài tập 40 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ABCD là hình chữ nhật. Chứng minh rằng:
a) (SAB) ⊥ (SBC);
b) (SAD) ⊥ (SCD).
-
Bài tập 41 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp S.ABCD có ABCD là hình thoi, (SAC) ⊥ (ABCD), (SBD) ⊥ (ABCD). Chứng minh rằng (SAC) ⊥ (SBD)?
-
Bài tập 42 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp S.ABC có Gọi H là trực tâm tam giác ABC.Chứng minh rằng (SAH) ⊥ (ABC)?
-
Bài tập 43 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp S.ABCD có ABCD là hình vuông, tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Chứng minh rằng:
a) (SAD) ⊥ (SAB);
b) (SBC) ⊥ (SAB);
c) (SAD) ⊥ (SBC).
-
Bài tập 44 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, (SAC) ⊥ (ABCD). Gọi M là trung điểm của AD, (SBM) ⊥ (ABCD). Giả sử SA = 5a, AB = 3a, AD = 4a và góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng φ. Tính cosφ?






