Bài tập 40 trang 104 SBT Toán 11 Tập 2 Cánh diều
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ABCD là hình chữ nhật. Chứng minh rằng:
a) (SAB) ⊥ (SBC);
b) (SAD) ⊥ (SCD).
Hướng dẫn giải chi tiết Bài tập 40
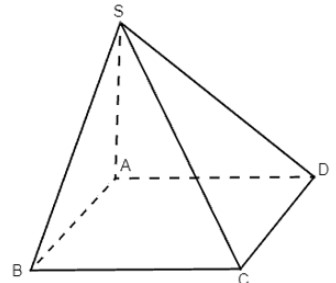
a) Ta có: SA ⊥ (ABCD), BC ⊂ (ABCD) suy ra SA ⊥ BC.
Vì ABCD là hình chữ nhật nên BC ⊥ AB.
Ta có: BC ⊥ SA, BC ⊥ AB, SA ∩ AB = A trong (SAB)
Suy ra BC ⊥ (SAB).
Hơn nữa BC ⊂ (SBC)
Từ đó ta có: (SAB) ⊥ (SBC).
b) Ta có: SA ⊥ (ABCD), CD ⊂ (ABCD) suy ra SA ⊥ CD.
Vì ABCD là hình chữ nhật nên CD ⊥ AD.
Ta có: CD ⊥ SA, CD ⊥ AD, SA ∩ AD = A trong (SAD)
Suy ra CD ⊥ (SAD).
Hơn nữa CD ⊂ (SCD)
Từ đó ta có: (SAD) ⊥ (SCD).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





