Hoạt động 3 trang 97 SGK Toán 11 Tập 2 Cánh diều
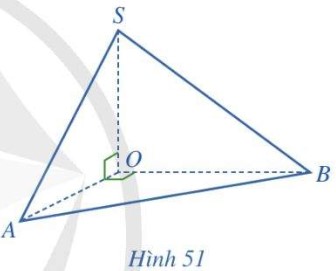
Cho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\), \(\widehat {AOS} = \widehat {AOB} = {90^ \circ }\) (Hình 51).
a) Giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) là đường thẳng nào?
b) \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) hay không?
c) \(SO\) có vuông góc với mặt phẳng \(\left( {AOB} \right)\) hay không?
Hướng dẫn giải chi tiết Hoạt động 3
a) Ta có:
\(\left. \begin{array}{l}A \in \left( {AOS} \right) \cap \left( {AOB} \right)\\O \in \left( {AOS} \right) \cap \left( {AOB} \right)\end{array} \right\} \Rightarrow AO = \left( {AOS} \right) \cap \left( {AOB} \right)\)
b) Ta có: \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
Vậy \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\).
c) Ta có: \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
\(\widehat {AOB} = {90^ \circ } \Rightarrow AO \bot BO\)
Vậy \(\widehat {SOB}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {S,AO,B} \right]\)
Vì \(\left( {AOS} \right) \bot \left( {AOB} \right)\) nên \(\widehat {SOB} = {90^ \circ }\)
\(\left. \begin{array}{l} \Rightarrow SO \bot OB\\SO \bot OA\end{array} \right\} \Rightarrow SO \bot \left( {AOB} \right)\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động 2 trang 96 SGK Toán 11 Tập 2 Cánh diều - CD
Luyện tập 2 trang 97 SGK Toán 11 Tập 2 Cánh diều - CD
Luyện tập 3 trang 97 SGK Toán 11 Tập 2 Cánh diều - CD
Hoạt động 4 trang 98 SGK Toán 11 Tập 2 Cánh diều - CD
Luyện tập 4 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 1 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 2 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 3 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 4 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 5 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 6 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài tập 33 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 34 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 35 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 36 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 37 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 38 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 39 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 40 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 41 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 42 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD





