Bài 3 trang 99 SGK Toán 11 Tập 2 Cánh diều
Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt còn lại.
Hướng dẫn giải chi tiết Bài 3
a)
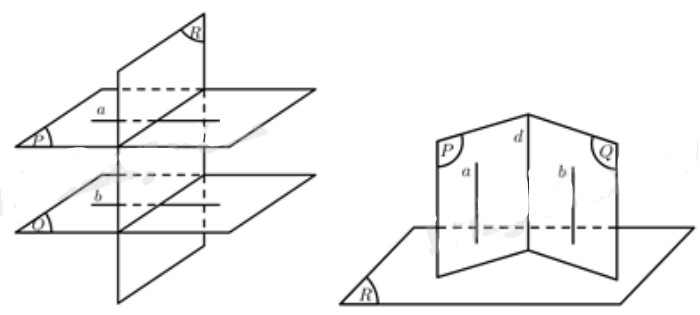
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Ta cần chứng minh \(\left( P \right)\parallel \left( Q \right)\) hoặc \(d \bot \left( R \right)\) với \(d = \left( P \right) \cap \left( Q \right)\).
Vì \(\left( P \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( R \right)\), \(\left( Q \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(b \subset \left( Q \right)\) sao cho \(b \bot \left( R \right)\)
\( \Rightarrow a\parallel b\)
Vậy \(\left( P \right)\parallel \left( Q \right)\) hoặc nếu \(\left( P \right),\left( Q \right)\) cắt nhau theo giao tuyến \(d\) thì \(d\parallel a \Rightarrow d \bot \left( R \right)\).
b)
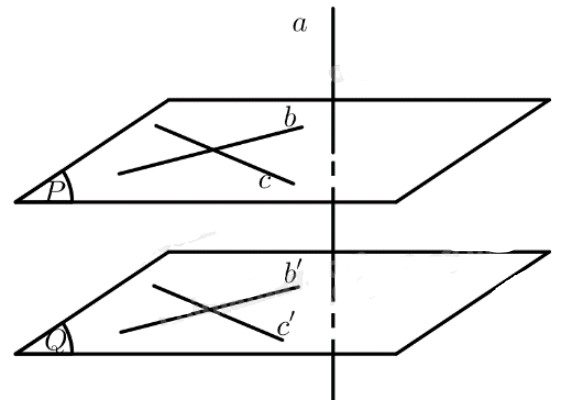
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) song song với nhau và đường thẳng \(a\) vuông góc với \(\left( P \right)\). Ta cần chứng minh \(a \bot \left( Q \right)\).
Trên \(\left( P \right)\) lấy hai đường thẳng \(b,c\) cắt nhau, trên \(\left( Q \right)\) lấy hai đường thẳng \(b',c'\) sao cho \(b'\parallel b,c'\parallel c\).
Vì \(b,c\) cắt nhau nên \(b',c'\) cắt nhau.
\(\begin{array}{l}\left. \begin{array}{l}a \bot \left( P \right) \Rightarrow a \bot b,a \bot c\\b\parallel b',c\parallel c'\end{array} \right\} \Rightarrow a \bot b',a \bot c'\\ \Rightarrow a \bot \left( Q \right)\end{array}\)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài 1 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 2 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 4 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 5 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 6 trang 99 SGK Toán 11 Tập 2 Cánh diều - CD
Bài tập 33 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 34 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 35 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 36 trang 103 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 37 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 38 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 39 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 40 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 41 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 42 trang 104 SBT Toán 11 Tập 2 Cánh diều - CD





