Bài tập 44 trang 104 SBT Toán 11 Tập 2 Cánh diều
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, (SAC) ⊥ (ABCD). Gọi M là trung điểm của AD, (SBM) ⊥ (ABCD). Giả sử SA = 5a, AB = 3a, AD = 4a và góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng φ. Tính cosφ?
Hướng dẫn giải chi tiết Bài tập 44
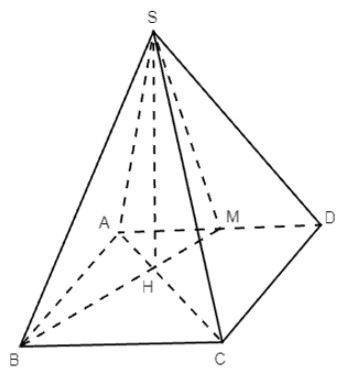
Gọi H là giao điểm của BM và AC.
Suy ra: H ∈ BM ⊂ (SBM) và H ∈ AC ⊂ (SAC) nên ta có H ∈ (SBM) ∩ (SAC).
Mà S ∈ (SBM) ∩ (SAC).
Từ đó suy ra: SH = (SBM) ∩ (SAC).
Ta có: (SAC) ⊥ (ABCD), (SBM) ⊥ (ABCD), SH = (SBM) ∩ (SAC).
Suy ra SH ⊥ (ABCD), tức H là hình chiếu vuông góc của S trên (ABCD).
Nên góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng SA và AH và bằng
Do ABCD là hình chữ nhật nên
Áp dụng định lí Pythagore trong tam giác ADC vuông tại D có:
AC2 = AD2 + DC2
(vì DC = AB do ABCD là hình chữ nhật).
Do M là trung điểm của AD nên
Do ABCD là hình chữ nhật nên AD // BC hay AM // BC.
Áp dụng hệ quả định lí Thalès với AM // BC ta có:
Vì SH ⊥ (ABCD) và AH ⊂ (ABCD) nên SH ⊥ AH.
Xét tam giác SAH vuông tại H có:
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





