Hãy tưởng tượng rằng bạn đang trên một chiếc tàu vũ trụ tốc độ ánh sáng, bay đi qua các hành tinh và vũ trụ vô tận. Bạn nhìn ra khung cảnh và thấy nhiều điểm lấp lánh trên bầu trời. Đó chính không gian ba chiều mà chúng ta sắp được khám phá và tìm hiểu ngay sau đây. Cùng HOC247 khám phá thế giới của Điểm, đường thẳng và mặt phẳng trong Toán 11 Chân trời sáng tạo một cách vui nhộn nhé!
Tóm tắt lý thuyết
1.1. Mặt phẳng trong không gian
Điểm, đường thăng và mặt phẳng là ba đối tượng cơ bản của hình học không gian.
Mặt bảng, mặt bản, mặt sàn nhà, mặt hồ nước yên lặng cho ta hình ảnh một phần của một mặt phẳng. Mặt phẳng không có bề dày và không có giới hạn.
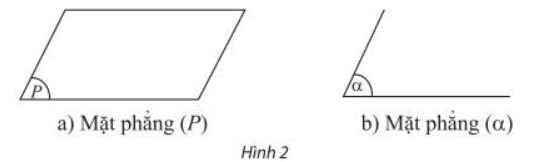
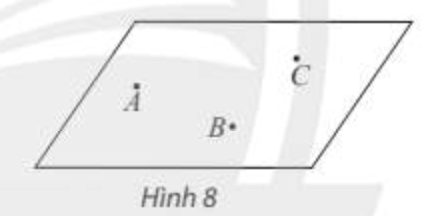
Ta thường dùng hình bình hành hay một miền góc để biểu diễn mặt phẳng và dùng chữ cái in hoa hoặc chữ cái Hy Lạp trong dấu ngoặc để kí hiệu mặt phẳng.
Chú ý: Mặt phẳng (P) còn được viết tắt là mp(P) hoặc (P).
a) Điểm thuộc mặt phẳng
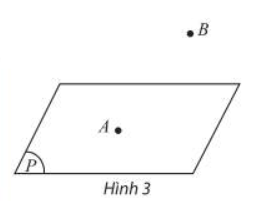
Cho hai điểm A, B và mặt phẳng (P) như Hình 3.
- Nếu điểm A thuộc mặt phẳng (P) thì ta nói A nằm trên (P) hay (P) chứa A, hay (P) đi qua A và kí hiệu là A \(\in\) (P).
- Nếu điểm B không thuộc mặt phẳng (P) thì ta nói B nằm ngoài (P) hay (P) không chứa B và kí hiệu là B \(\notin\) (P).
b) Biểu diễn các hình trong không gian lên một mặt phẳng
Ta thường dựa vào các quy tắc sau:
– Hình biểu diễn của đường thẳng là đường thăng, của đoạn thẳng là đoạn thẳng.
– Giữ nguyên tính liên thuộc (thuộc hay không thuộc) giữa điểm với đường thẳng hoặc với đoạn thẳng.
– Giữ nguyên tính song song, tỉnh cắt nhau giữa các đường thẳng.
– Biểu diễn đường nhìn thấy bằng nét vẽ liền và biểu diễn đường bị che khuất bằng nét vẽ đứt đoạn.
1.2. Các tính chất được thừa nhận của hình học không gian
Tính chất 1:
Có một và chỉ một đường thẳng đi qua hai điểm
Tính chất 2:
Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Tính chất 3:
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tính chất 4:
Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
Chú ý: Nếu có nhiều điểm củng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng, còn nếu không có mặt phẳng nào chứa các điểm đó thì ta nói chúng không đồng phẳng.
Tính chất 5:
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Chú ý: Đường thẳng d chung của hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu d =(P)\(\cap\)(Q).
Tính chất 6:
Trong mỗi mặt phẳng, các kết quả đã biết của hình học phẳng đều đúng.
1.3. Cách xác định mặt phẳng
- Một mặt phẳng được xác định nếu biết nó chứa ba điểm không thẳng hàng.
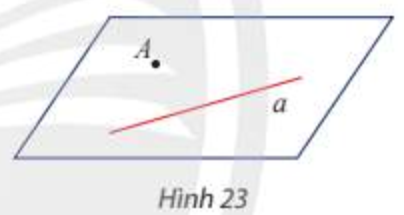
- Một mặt phẳng được xác định nếu biết nó chứa một đường thẳng và một điểm không thuộc đường thẳng đó.
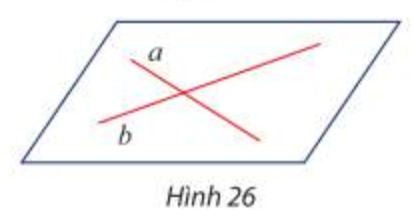
- Một mặt phẳng được xác định nếu biết nó chứa hai đường thẳng cắt nhau.
1.4. Hình chóp và hình tứ diện
a) Hình chóp
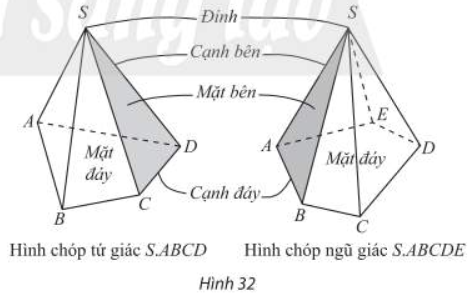
Cho đa giác lồi n cạnh nằm trong mặt phẳng (\(\alpha\)) và điểm S không thuộc (\(\alpha\)). Nối S với các đỉnh của đa giác đó, ta được n tam giác. Hình tạo bởi n tam giác đó và đa giác lồi n cạnh được gọi là hình chóp, kí hiệu S.A1A2...An
Trong hình chóp S.A1A2...An ta gọi tên các đối tượng như hình sau:
b) Tứ diện
Cho bốn điểm A, B, C, D không đồng phẳng. Hình tạo bởi bốn tam giác ABC, ACD, ADB và BCD được gọi là hình tứ diện (hay tứ diện), kí hiệu ABCD.
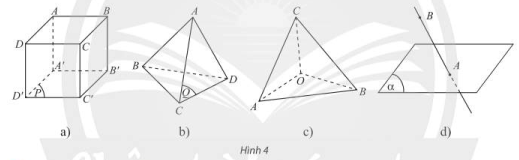
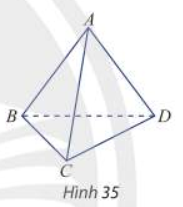
Trong tứ diện ABCD (Hình 35), ta gọi:
- Các điểm A, B, C, D là các đỉnh.
- Các đoạn thẳng AB, AC, AD, BC, CD. BD là các cạnh của tứ diện.
- Hai cạnh không đi qua một đỉnh là hai cạnh đối diện.
- Các tam giác ABC, ACD, ADB, BCD là các mặt của tứ diện.
- Đỉnh không thuộc một mặt của tứ diện là đỉnh đối diện với mặt đó.
Chú ý:
+ Hình tứ diện có bốn mặt là các tam giác đều được gọi là hình tử diện đều.
+ Một tứ diện có thể xem như là một hình chóp tam giác với đỉnh là một đỉnh tuỳ ý của tứ diện và đáy là mặt của tứ diện không chứa đỉnh đó.
Bài tập minh họa
Câu 1. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Giao tuyến của \(\left( SAC \right)\) và \(\left( SBD \right)\) là
Hướng dẫn giải
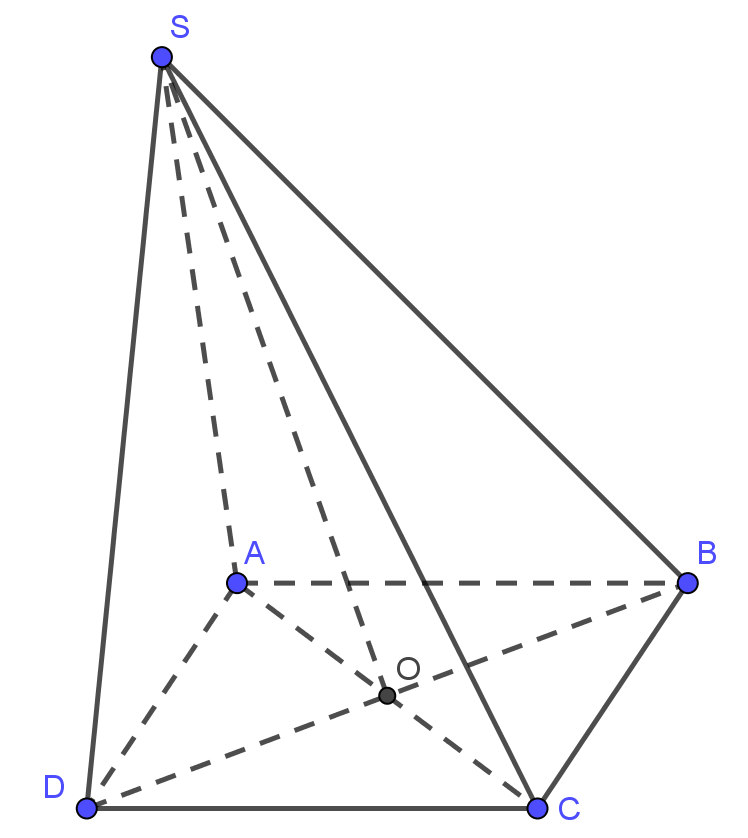
Hai mặt phẳng \(\left( SAC \right)\) và \(\left( SBD \right)\) có điểm chung thứ nhất là điểm \(S\);
\(O\) là giao điểm của \(AC\) và \(BD\) nên là điểm chung thứ hai.
Do đó, \(SO\) là giao tuyến của hai mặt phẳng \(\left( SAC \right)\) và \(\left( SBD \right)\).
Câu 2. Cho tứ diện \(ABCD\). Gọi \(O\) là điểm bên trong tam giác \(BCD\) và \(M\) là điểm trên đoạn \(AO\). Gọi \(I,J\) là hai điểm trên cạnh \(BC,BD\). Giả sử \(IJ\) cắt \(CD\) tại \(K\), \(BO\) cắt \(IJ\) tại \(E\)và \(BO\) cắt \(CD\) tại \(H\),\(ME\) cắt \(AH\) tại \(F\). Giao tuyến của hai mặt phẳng \(\left( MIJ \right)\) và \(\left( ACD \right)\) là đường thẳng
A. \(KM\). B. \(KF\). C. \(AK\). D. \(MF\).
Hướng dẫn giải
Chọn B
%20v%C3%A0%20(%20ACD)%20l%C3%A0%20%C4%91%C6%B0%E1%BB%9Dng%20th%E1%BA%B3ng.png)
Xét mặt phẳng \(\left( MIJ \right)\) và \(\left( ACD \right)\) có
+ \(IJ\cap CD=K\) \(\Rightarrow \) \(K\) chung.
+ \(ME\cap AH=F\) \(\Rightarrow \) \(F\) chung.
Suy ra \(\left( MIJ \right)\cap \left( ACD \right)=KF\)
Luyện tập Bài 1 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Mô tả được cách xác định mặt phẳng, giao tuyến giữa hai mặt phẳng, các tính chất thừa nhận trong không gian.
- Nhận biết được hình chóp, hình tứ diện.
3.1. Trắc nghiệm Bài 1 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 4 Bài 1 cực hay có đáp án và lời giải chi tiết.
-
- A. Hai đường thẳng cắt nhau
- B. Bốn điểm phân biệt.
- C. Một điểm và một đường thẳng.
- D. Ba điểm phân biệt.
-
- A. Hình chóp có tất cả các mặt là hình tam giác.
- B. Số cạnh bên của hình chóp bằng số mặt của nó.
- C. Tồn tại một mặt bên của hình chóp không là tam giác.
- D. Tất cả mặt bên của hình chóp là hình tam giác.
-
Câu 3:
Trong không gian có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?
- A. 2
- B. 3
- C. 4
- D. 1
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 1 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 4 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 88 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 88 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 89 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 89 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 90 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 90 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 90 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 90 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 91 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 5 trang 91 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 5 trang 91 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 6 trang 92 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 6 trang 92 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 7 trang 92 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 93 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 8 trang 94 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 9 trang 95 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 7 trang 95 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 95 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 3 trang 95 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 10 trang 96 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 11 trang 96 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 8 trang 98 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 4 trang 98 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 5 trang 98 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 1 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247