Bài tập 1 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo
Cho hình chóp S.ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD.
a) Tìm giao điểm của EF và (SAC);
b) Tìm giao điểm của BC và (AEF).
Hướng dẫn giải chi tiết Bài tập 1
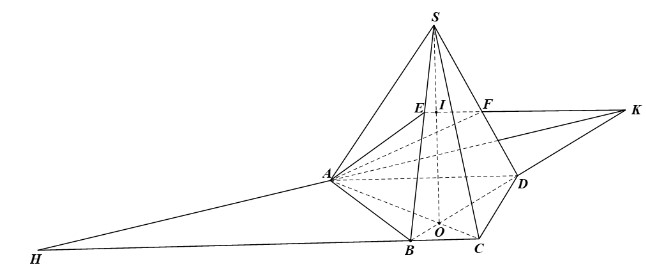
a) - Trong mặt phẳng (ABCD), gọi O = AC ∩ BD.
Ta có: O ∈ AC, AC ⊂ (SAC) nên O ∈ (SAC).
O ∈ BD, BD ⊂ (SBD) nên O ∈ (SBD).
Do đó O ∈ (SAC) ∩ (SBD).
- Lại có S ∈ (SAC) và S ∈ (SBD) nên S ∈ (SAC) ∩ (SBD).
Suy ra (SAC) ∩ (SBD) = SO.
Trong mặt phẳng (SBD), gọi I = EF ∩ SO.
Ta có: I ∈ SO, SO ⊂ (SAC) nên I ∈ (SAC).
Vậy EF ∩ (SAC) = I.
b) - Trong mặt phẳng (SBD), gọi K = EF ∩ BD.
Ta có: K ∈ EF, EF ⊂ (AEF) nên K ∈ (AEF);
K ∈ BD, BD ⊂ (ABCD) nên K ∈ (ABCD).
Do đó K ∈ (ABCD) ∩ (AEF).
Lại có A ∈ (ABCD) và A ∈ (AEF) nên A = (ABCD) ∩ (AEF).
Suy ra (ABCD) ∩ (AEF) = AK.
- Trong mặt phẳng (ABCD), gọi H = BC ∩ AK.
Ta có: H ∈ AK, AK ⊂ (AEF) nên H ∈ (AEF).
Vậy BC ∩ (AEF) = H.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 4 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 99 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 2 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST





