Bài tập 4 trang 112 SBT Toán 11 Tập 1 Chân trời sáng tạo
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho EB > AE, AF > FC, BG > GD. Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD)?
Hướng dẫn giải chi tiết Bài tập 4
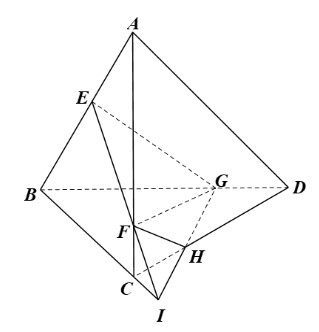
- Ta có EF ⊂ (ABC) và EF ⊂ (EFG) nên (EFG) ∩ (ABC) = EF.
- Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD.
Ta có: H ∈ IG, mà IG ⊂ (EFG) nên H ∈ (EFG).
Lại có F ∈ (EFG) nên FH ⊂ (EFG). (1)
Ta cũng có: F ∈ AC, mà AC ⊂ (ACD).
H ∈ CD, mà CD ⊂ (ACD).
Do đó FH ⊂ (ACD). (2)
Từ (1) và (2) suy ra (EFG) ∩ (ACD) = FH.
- Tương tự, ta cũng có:
HG ⊂ (EFG) và HG ⊂ (BCD) nên (EFG) ∩ (BCD) = HG;
GE ⊂ (EFG) và GE ⊂ (ABD) nên (EFG) ∩ (ABD) = GE.
Vậy (EFG) ∩ (ACD) = FH, (EFG) ∩ (BCD) = HG, (EFG) ∩ (ABD) = GE.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





