Giải bài 5 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2
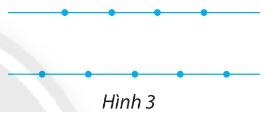
Cho 9 điểm nằm trên hai đường thẳng song song như hình 3. Có bao nhiêu tam giác có các đỉnh là ba điểm trong các điểm đã cho?
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Tam giác được tạo thành từ 3 điểm không thẳng hàng
=> chọn 2 điểm ở đường này và 1 điểm ở đường kia.
Lời giải chi tiết
Cách 1:
TH 1: Chọn 2 điểm thuộc đường thẳng có 4 điểm
Chọn 2 điểm từ đường thẳng trên có \(C_4^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 5 cách
=> Số tam giác tạo thành là \(5.C_4^2 = 30\)
TH 2: Chọn 2 điểm thuộc đường thẳng có 5 điểm
Chọn 2 điểm từ đường thẳng dưới có \(C_5^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 4 cách
=> Số tam giác tạo thành là \(4.C_5^2 = 40\)
Vậy có tất cả 70 tam giác được tạo thành.
Cách 2:
Số cách chọn 3 điểm bất kì là: \(C_9^3 = 84\) cách
Số cách chọn 3 điểm thẳng hàng là: \(C_4^3 +C_5^3 =14 \) cách
=> Số cách chọn 3 điểm không thẳng hàng là: 84 - 14 = 70 (cách)
Do đó ta có thể có 70 tam giác.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 3 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 36 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Câu 1 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Câu 2 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Câu 3 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Câu 4 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Câu 5 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 48 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 49 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 49 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST