Giải bài 1 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho bất phương trình bậc nhất hai ẩn \(x - 2y + 6 > 0\)
a) (0;0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của các bất phương trình đã cho trên mặt phẳng tọa độ Oxy
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
a) Xét (0 ; 0) có là nghiệm của bất phương trình đã cho.
b) Xét cặp điểm thuộc bất phương trình bậc nhất hai ẩn \(x - 2y + 6 > 0\)
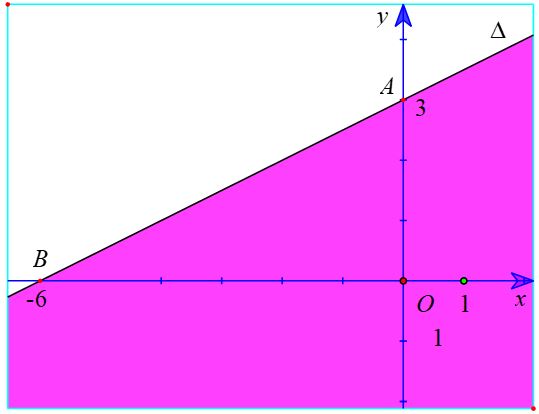
c) Vẽ đường thẳng ∆ : x – 2y + 6 = 0 đi qua hai điểm A(0; 3); B(-6; 0). Xét gốc tọa độ O(0 ; 0).
Lời giải chi tiết
a) Với cặp (0 ; 0) ta có : 0 – 2.0 + 6 = 6 > 0 nên (0 ; 0) là nghiệm của bất phương trình đã cho.
Vậy (0 ; 0) là một nghiệm của bất phương trình bậc nhất hai ẩn \(x - 2y + 6 > 0\)
b)
+ Lấy cặp số (1 ; 0) ta có 1 – 2.0 + 6 = 7 > 0 nên cặp số (1 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (0 ; 1) ta có 0 – 2.1 + 6 = 4 > 0 nên cặp số (0 ; 1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (-1 ; -1) ta có –1 – 2. (–1) + 6 = 7 > 0 nên cặp số (-1 ; -1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
Vậy ta có ba cặp số (1 ; 0) ; (0 ; 1) ; (-1 ; -1) đều là nghiệm của bất phương trình x - 2y + 6 > 0.
c) Vẽ đường thẳng ∆ : x – 2y + 6 = 0 đi qua hai điểm A(0; 3); B(-6; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và (0 ; 0) là một nghiệm của bất phương trình
x - 2y + 6 > 0.
Do đó, miền nghiệm của bất phương trình x - 2y + 6 > 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền được tô màu trong hình sau).
-- Mod Toán 10 HỌC247
-


A. x + y – 3 > 0;
B. – x – y < 0;
C. x + 3y + 1< 0;
D. – x – 3y – 1 < 0.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Thực hành 3 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 32 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 27 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 27 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 27 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 27 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST