Giải bài tập Toán 10 Chân trời sáng tạo Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Thời gian hoàn thành bài chạy 5 km (tính theo phút) của hai nhóm thanh niên được cho ở bảng sau:

a) Hãy tính độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong từng nhóm.

b) Nhóm nào có thành tích chạy đồng đều hơn?

Hãy tìm khoảng biến thiên và khoảng tứ phân vị của các mẫu số liệu sau:

a) \(10;13;15;2;10;19;2;5;7\)

b) \(15;19;10;5;9;10;1;2;5;15\)

Dưới đây là bảng số liệu thống kê của Biểu đồ nhiệt trung bình các tháng trong 2019 của hai tình Lai Châu và Lâm Đồng (được đề cập đến ở hoạt động khởi động của bài học)

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm đồng.

b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.

Hãy tìm giá trị ngoại lệ của mẫu số liệu: 37; 12; 3; 9; 10; 9; 12; 3; 10.

Hai cung thủ A và B đã ghi lại kết quả từng lần bắn của mình ở bảng sau:

a) Tính kết quả trung bình của mỗi cung thủ trên

b) Cung thủ nào có kết quả các lần bắn ổn định hơn?

Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.

a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.

b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.

Hãy chọn ngẫu nhiên trong lớp ra 5 bạn nam và 5 bạn nữ rồi do chiều cao các bạn đó. So sánh xem chiều cao của các bạn năm hay các bạn nữ đồng đều hơn.

Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và các giá trị ngoại lệ của các mẫu số liệu sau:

a) 6; 8; 3; 4; 5; 6; 7; 2; 4.

b) 13; 37; 64; 12; 26; 43; 29; 23.

Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị của các mẫu số liệu sau:

a)

b)

Hãy so sánh số trung bình, phương sai và độ lệch chuẩn của ba mẫu só liệu sau:

Mẫu 1: 0,1;  0,3;  0,5;  0,5;  0,3;  0,7.

Mẫu 2: 1,1;  1, 3;  1,5;  1,5;  1,3; 1,7.

Mẫu 3: 1;       3;     5;     5;       3;    7.

Sản lượng lúa các năm từ 2014 đến 2018 của hai tỉnh Thái Bình và Hậu Giang được cho ở bảng sau (đơn vị nghìn tấn):

a) Hãy tính độ lệch chuẩn và khoảng biến thiên của sản lượng lúa từng tỉnh.

b) Tỉnh nào có sản lượng lúa ổn định hơn? Tại sao?

Kết quả điều tra mức lương hằng tháng của một số công nhân của hai nhà máy A và B được cho ở bảng sau (đơn vị: triệu đồng):

a) Hãy tìm số trung bình, mốt, tứ phân vị và độ lệch chuẩn của hai mẫu số liệu lấy từ nhà máy A và nhà máy B.

b) Hãy tìm các giá trị ngoại lệ trong mỗi mẫu số liệu trên. Công nhân nhà máy nào có mức lương cao hơn? Tại sao?

Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu sau:

a)     90;     56;     50;     45;     46;     48;     52;     43.

b)    19;     11;     1;       16;     19;     12;     14;     10;     11.

c)     6,7;    6,2;    9,7;    6,3;    6,8;    6,1;    6,2.

d)    0,79;  0,68;  0,35;  0,38;  0,05;  0,35.

Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lên (nếu có) của mỗi mẫu số liệu cho bởi bảng tần số sau:

a)

b)

Một kĩ thuật viên thống kê lại số lần máy bị lỗi từng ngày trong tháng 5/2021 ở bảng sau:

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu

b) Xác định các giá trị ngoại lệ (nếu có) của mẫu số liệu

c) Hãy tìm phương sai và độ lệch chuẩn của mẫu số liệu.

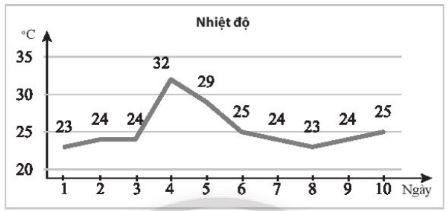
Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: 0C)

a) Hãy tìm viết mẫu số liệu thống kê nhiệt độ từ biểu đồ trên.

b) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.

c) Hãy tìm phương sai và độ lệch chuẩn của mẫu số liệu đó.

Khuê và Trọng ghi lại số tin nhắn điện thoại mà mỗi người nhận được từ ngày 1/9 đến ngày 15/9 năm 2020 ở bảng sau:

a) Hãy tìm phương sai của từng dãy số liệu.

b) Sau khi bỏ đi các giá trị ngoại lệ (nếu có), hãy so sánh số lượng tin nhắn mỗi bạn nhận được theo số trung bình và theo trung vị.

Bảng sau ghi giá bán ra lúc 11 giờ trưa của 2 mã cổ phiếu A và B trong 10 ngày liên tiếp (đơn vị: nghìn đồng).

a) Biết có 1 trong 10 ngày trên có sự bất thường trong giá cổ phiếu. Hãy tìm ngày đó và giải thích.

b) Sau khi bỏ đi ngày có giá bất thường, hãy cho biết giá cổ phiếu nào ổn định hơn. Tại sao?